In computer science, an abstract data type (ADT) is a mathematical model for data types, defined by its behavior (semantics) from the point of view of a user of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations. This mathematical model contrasts with data structures, which are concrete representations of data, and are the point of view of an implementer, not a user. For example, a stack has push/pop operations that follow a Last-In-First-Out rule, and can be concretely implemented using either a list or an array. Another example is a set which stores values, without any particular order, and no repeated values. Values themselves are not retrieved from sets, rather one tests a value for membership to obtain a Boolean "in" or "not in".

In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. That is, it is a k-ary tree with k = 2. A recursive definition using set theory is that a binary tree is a tuple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set containing the root.
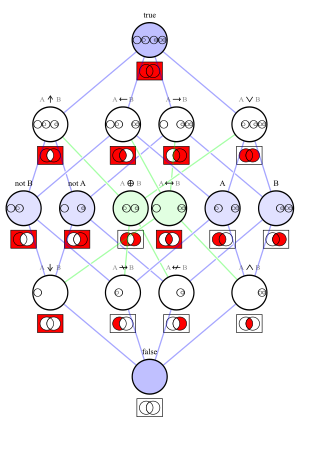
In logic, a logical connective is a logical constant. Connectives can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary connective can be used to join the two atomic formulas and , rendering the complex formula .
The SECD machine is a highly influential virtual machine and abstract machine intended as a target for functional programming language compilers. The letters stand for Stack, Environment, Control, Dump—the internal registers of the machine. The registers Stack, Control, and Dump point to stacks, and Environment points to an associative array.
In logic, mathematics, and computer science, arity is the number of arguments or operands taken by a function, operation or relation. In mathematics, arity may also be called rank, but this word can have many other meanings. In logic and philosophy, arity may also be called adicity and degree. In linguistics, it is usually named valency.
In mathematics, an algebraic structure consists of a nonempty set A, a collection of operations on A, and a finite set of identities, known as axioms, that these operations must satisfy.
In computer science, a binary decision diagram (BDD) or branching program is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed representation of sets or relations. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression.
In computer science, tree traversal is a form of graph traversal and refers to the process of visiting each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.
In logic, a truth function is a function that accepts truth values as input and produces a unique truth value as output. In other words: the input and output of a truth function are all truth values; a truth function will always output exactly one truth value, and inputting the same truth value(s) will always output the same truth value. The typical example is in propositional logic, wherein a compound statement is constructed using individual statements connected by logical connectives; if the truth value of the compound statement is entirely determined by the truth value(s) of the constituent statement(s), the compound statement is called a truth function, and any logical connectives used are said to be truth functional.
Laws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy. LoF describes three distinct logical systems:

In computer science, an in-tree or parent pointer tree is an N-ary tree data structure in which each node has a pointer to its parent node, but no pointers to child nodes. When used to implement a set of stacks, the structure is called a spaghetti stack, cactus stack or saguaro stack. Parent pointer trees are also used as disjoint-set data structures.
In computer science, the shunting yard algorithm is a method for parsing arithmetical or logical expressions, or a combination of both, specified in infix notation. It can produce either a postfix notation string, also known as Reverse Polish notation (RPN), or an abstract syntax tree (AST). The algorithm was invented by Edsger Dijkstra and named the "shunting yard" algorithm because its operation resembles that of a railroad shunting yard. Dijkstra first described the shunting yard algorithm in the Mathematisch Centrum report MR 34/61.

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.
The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.
In logic, a functionally complete set of logical connectives or Boolean operators is one that can be used to express all possible truth tables by combining members of the set into a Boolean expression. A well-known complete set of connectives is { AND, NOT }. Each of the singleton sets { NAND } and { NOR } is functionally complete. However, the set { AND, OR } is incomplete, due to its inability to express NOT.
Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.
The logic alphabet, also called the X-stem Logic Alphabet (XLA), constitutes an iconic set of symbols that systematically represents the sixteen possible binary truth functions of logic. The logic alphabet was developed by Shea Zellweger. The major emphasis of his iconic "logic alphabet" is to provide a more cognitively ergonomic notation for logic. Zellweger's visually iconic system more readily reveals, to the novice and expert alike, the underlying symmetry relationships and geometric properties of the sixteen binary connectives within Boolean algebra.
In mathematical logic, a term denotes a mathematical object while a formula denotes a mathematical fact. In particular, terms appear as components of a formula. This is analogous to natural language, where a noun phrase refers to an object and a whole sentence refers to a fact.
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arguments, that is, for each combination of values taken by their logical variables. In particular, truth tables can be used to show whether a propositional expression is true for all legitimate input values, that is, logically valid.
In computer science, parallel tree contraction is a broadly applicable technique for the parallel solution of a large number of tree problems, and is used as an algorithm design technique for the design of a large number of parallel graph algorithms. Parallel tree contraction was introduced by Gary L. Miller and John H. Reif, and has subsequently been modified to improve efficiency by X. He and Y. Yesha, Hillel Gazit, Gary L. Miller and Shang-Hua Teng and many others.
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values true and false, usually denoted 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as conjunction (and) denoted as ∧, disjunction (or) denoted as ∨, and the negation (not) denoted as ¬. Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations, in the same way that elementary algebra describes numerical operations.
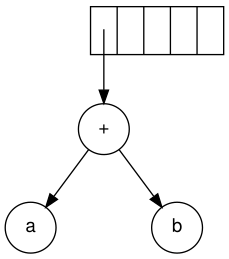


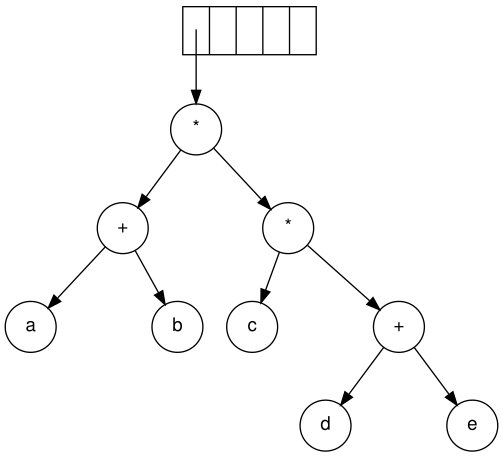

![Binary boolean expression tree equivalent to ((true
[?]
{\displaystyle \lor }
false)
[?]
{\displaystyle \land }
!
{\displaystyle \neg }
false)
[?]
{\displaystyle \lor }
(true
[?]
{\displaystyle \lor }
false)) Exp-tree-ex-13.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/a/a1/Exp-tree-ex-13.svg/270px-Exp-tree-ex-13.svg.png)






