In quantum mechanics, bra–ket notation is a standard notation for describing quantum states. It can also be used to denote abstract vectors and linear functionals in mathematics. The notation uses angle brackets and a vertical bar, to denote the scalar product of vectors or the action of a linear functional on a vector in a complex vector space. The scalar product or action is written as
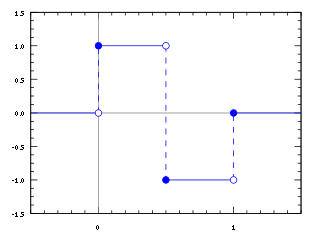
In mathematics, the Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal basis. The Haar sequence is now recognised as the first known wavelet basis and extensively used as a teaching example.

A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it. The most common symbols for a wave function are the Greek letters ψ or Ψ.
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal and unit vectors. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length. An orthonormal set which forms a basis is called an orthonormal basis.
Pseudo-spectral methods, also known as discrete variable representation (DVR) methods, are a class of numerical methods used in applied mathematics and scientific computing for the solution of partial differential equations. They are closely related to spectral methods, but complement the basis by an additional pseudo-spectral basis, which allows representation of functions on a quadrature grid. This simplifies the evaluation of certain operators, and can considerably speed up the calculation when using fast algorithms such as the fast Fourier transform.
The Fast Wavelet Transform is a mathematical algorithm designed to turn a waveform or signal in the time domain into a sequence of coefficients based on an orthogonal basis of small finite waves, or wavelets. The transform can be easily extended to multidimensional signals, such as images, where the time domain is replaced with the space domain. This algorithm was introduced in 1989 by Stéphane Mallat.

Coiflets are discrete wavelets designed by Ingrid Daubechies, at the request of Ronald Coifman, to have scaling functions with vanishing moments. The wavelet is near symmetric, their wavelet functions have vanishing moments and scaling functions , and has been used in many applications using Calderón-Zygmund Operators.
An orthogonal wavelet is a wavelet whose associated wavelet transform is orthogonal. That is, the inverse wavelet transform is the adjoint of the wavelet transform. If this condition is weakened one may end up with biorthogonal wavelets.
In mathematics, a dual wavelet is the dual to a wavelet. In general, the wavelet series generated by a square integrable function will have a dual series, in the sense of the Riesz representation theorem. However, the dual series is not itself in general representable by a square integrable function.

In analytical mechanics, a branch of theoretical physics, Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by Edward John Routh. Correspondingly, the Routhian is the function which replaces both the Lagrangian and Hamiltonian functions.
In functional analysis and quantum measurement theory, a positive-operator valued measure (POVM) is a measure whose values are non-negative self-adjoint operators on a Hilbert space, and whose integral is the identity operator. It is the most general formulation of measurements in quantum physics. Since projective measurements on a large system—i.e., measurements that are performed mathematically by a projection-valued measure (PVM)—will act on a subsystem in ways that cannot be described by a PVM on the subsystem alone, the POVM formalism becomes necessary. POVMs are used in the field of quantum information.
In mathematics, in the area of wavelet analysis, a refinable function is a function which fulfils some kind of self-similarity. A function is called refinable with respect to the mask if
In quantum mechanics, the case of a particle in a one-dimensional ring is similar to the particle in a box. The particle follows the path of a semicircle from to where it cannot escape, because the potential from to is infinite. Instead there is total reflection, meaning the particle bounces back and forth between to . The Schrödinger equation for a free particle which is restricted to a semicircle is
In general relativity, the Vaidya metric describes the non-empty external spacetime of a spherically symmetric and nonrotating star which is either emitting or absorbing null dusts. It is named after the Indian physicist Prahalad Chunnilal Vaidya and constitutes the simplest non-static generalization of the non-radiative Schwarzschild solution to Einstein's field equation, and therefore is also called the "radiating(shining) Schwarzschild metric".
In mathematics, a biorthogonal polynomial is a polynomial that is orthogonal to several different measures. Biorthogonal polynomials are a generalization of orthogonal polynomials and share many of their properties. There are two different concepts of biorthogonal polynomials in the literature: Iserles & Nørsett (1988) introduced the concept of polynomials biorthogonal with respect to a sequence of measures, while Szegő introduced the concept of two sequences of polynomials that are biorthogonal with respect to each other.
In general relativity, the Weyl metrics are a class of static and axisymmetric solutions to Einstein's field equation. Three members in the renowned Kerr–Newman family solutions, namely the Schwarzschild, nonextremal Reissner–Nordström and extremal Reissner–Nordström metrics, can be identified as Weyl-type metrics.
In applied mathematical analysis, shearlets are a multiscale framework which allows efficient encoding of anisotropic features in multivariate problem classes. Originally, shearlets were introduced in 2006 for the analysis and sparse approximation of functions . They are a natural extension of wavelets, to accommodate the fact that multivariate functions are typically governed by anisotropic features such as edges in images, since wavelets, as isotropic objects, are not capable of capturing such phenomena.
In mathematics, in functional analysis, several different wavelets are known by the name Poisson wavelet. In one context, the term "Poisson wavelet" is used to denote a family of wavelets labeled by the set of positive integers, the members of which are associated with the Poisson probability distribution. These wavelets were first defined and studied by Karlene A. Kosanovich, Allan R. Moser and Michael J. Piovoso in 1995–96. In another context, the term refers to a certain wavelet which involves a form of the Poisson integral kernel. In a still another context, the terminology is used to describe a family of complex wavelets indexed by positive integers which are connected with the derivatives of the Poisson integral kernel.