 |
In finance, a Bond+Option is a capital guarantee product that provides an investor with a fixed, predetermined participation to an option. Buying the zero-coupon bond ensures the guarantee of the capital, and the remaining proceeds are used to buy an option. [1] [2]
As an example, we can consider a bond+call on 5 years, with Nokia as an underlying. Say it is a USD currency option, and that 5 year rates are 4.7%. That gives you a zero-coupon bond price of .
Say we are counting in units of $100. We then have to buy $79.06 worth of bonds to guarantee the 100 to be repaid at maturity, and we have $20.94 to spend on an option. Now the option price is unlikely to be exactly equal to 20.94 in this case, and it really depends on the underlying. Say we are using the Black–Scholes price for the call, and that we strike the option at the money, the volatility is the defining part here. A call on an underlying with implied volatility of 25% will give you a Black–Scholes price of $15.7 while with a volatility of 45%, you'd have to pay $21.76. [3]
Hence the participation would be the proportion you can get with the money you have.
The alternative is to simply buy the bond, which would return $126.49.
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a unique price given the risk of the security and its expected return. The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited.
In financial mathematics, put–call parity defines a relationship between the price of a European call option and European put option, both with the identical strike price and expiry, namely that a portfolio of a long call option and a short put option is equivalent to a single forward contract at this strike price and expiry. This is because if the price at expiry is above the strike price, the call will be exercised, while if it is below, the put will be exercised, and thus in either case one unit of the asset will be purchased for the strike price, exactly as in a forward contract.
An interest rate cap is a type of interest rate derivative in which the buyer receives payments at the end of each period in which the interest rate exceeds the agreed strike price. An example of a cap would be an agreement to receive a payment for each month the LIBOR rate exceeds 2.5%.
In finance, the style or family of an option is the class into which the option falls, usually defined by the dates on which the option may be exercised. The vast majority of options are either European or American (style) options. These options—as well as others where the payoff is calculated similarly—are referred to as "vanilla options". Options where the payoff is calculated differently are categorized as "exotic options". Exotic options can pose challenging problems in valuation and hedging.
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters. Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.
In financial mathematics, the implied volatility (IV) of an option contract is that value of the volatility of the underlying instrument which, when input in an option pricing model, will return a theoretical value equal to the current market price of said option. A non-option financial instrument that has embedded optionality, such as an interest rate cap, can also have an implied volatility. Implied volatility, a forward-looking and subjective measure, differs from historical volatility because the latter is calculated from known past returns of a security. To understand where implied volatility stands in terms of the underlying, implied volatility rank is used to understand its implied volatility from a one-year high and low IV.
In finance, moneyness is the relative position of the current price of an underlying asset with respect to the strike price of a derivative, most commonly a call option or a put option. Moneyness is firstly a three-fold classification:
In finance, a convertible bond or convertible note or convertible debt is a type of bond that the holder can convert into a specified number of shares of common stock in the issuing company or cash of equal value. It is a hybrid security with debt- and equity-like features. It originated in the mid-19th century, and was used by early speculators such as Jacob Little and Daniel Drew to counter market cornering.
Rational pricing is the assumption in financial economics that asset prices - and hence asset pricing models - will reflect the arbitrage-free price of the asset as any deviation from this price will be "arbitraged away". This assumption is useful in pricing fixed income securities, particularly bonds, and is fundamental to the pricing of derivative instruments.
Bond valuation is the determination of the fair price of a bond. As with any security or capital investment, the theoretical fair value of a bond is the present value of the stream of cash flows it is expected to generate. Hence, the value of a bond is obtained by discounting the bond's expected cash flows to the present using an appropriate discount rate.
In finance, a foreign exchange option is a derivative financial instrument that gives the right but not the obligation to exchange money denominated in one currency into another currency at a pre-agreed exchange rate on a specified date. See Foreign exchange derivative.
In finance, a bond option is an option to buy or sell a bond at a certain price on or before the option expiry date. These instruments are typically traded OTC.
In finance, a price (premium) is paid or received for purchasing or selling options. This article discusses the calculation of this premium in general. For further detail, see: Mathematical finance § Derivatives pricing: the Q world for discussion of the mathematics; Financial engineering for the implementation; as well as Financial modeling § Quantitative finance generally.
In finance, a butterfly is a limited risk, non-directional options strategy that is designed to have a high probability of earning a limited profit when the future volatility of the underlying asset is expected to be lower or higher than that asset's current implied volatility.
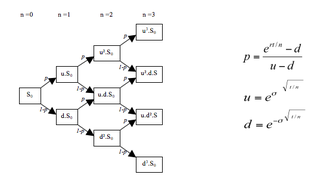
In finance, a lattice model is a technique applied to the valuation of derivatives, where a discrete time model is required. For equity options, a typical example would be pricing an American option, where a decision as to option exercise is required at "all" times before and including maturity. A continuous model, on the other hand, such as Black–Scholes, would only allow for the valuation of European options, where exercise is on the option's maturity date. For interest rate derivatives lattices are additionally useful in that they address many of the issues encountered with continuous models, such as pull to par. The method is also used for valuing certain exotic options, where because of path dependence in the payoff, Monte Carlo methods for option pricing fail to account for optimal decisions to terminate the derivative by early exercise, though methods now exist for solving this problem.
Constant proportion portfolio investment (CPPI) is a trading strategy that allows an investor to maintain an exposure to the upside potential of a risky asset while providing a capital guarantee against downside risk. The outcome of the CPPI strategy is somewhat similar to that of buying a call option, but does not use option contracts. Thus CPPI is sometimes referred to as a convex strategy, as opposed to a "concave strategy" like constant mix.
An equity-linked note (ELN) is a debt instrument, usually a bond, that differs from a standard fixed-income security in that the final payout is based on the return of the underlying equity, which can be a single stock, basket of stocks, or an equity index. Equity-linked notes are a type of structured products.
In finance, an option is a contract which conveys to its owner, the holder, the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset and have a valuation that may depend on a complex relationship between underlying asset price, time until expiration, market volatility, the risk-free rate of interest, and the strike price of the option. Options may be traded between private parties in over-the-counter (OTC) transactions, or they may be exchange-traded in live, public markets in the form of standardized contracts.
A reverse convertible security or convertible security is a short-term note linked to an underlying stock. The security offers a steady stream of income due to the payment of a high coupon rate. In addition, at maturity the owner will receive either 100% of the par value or, if the stock value falls, a predetermined number of shares of the underlying stock. In the context of structured product, a reverse convertible can be linked to an equity index or a basket of indices. In such case, the capital repayment at maturity is cash settled, either 100% of principal, or less if the underlying index falls conditional on barrier is hit in the case of barrier reverse convertibles.
In mathematical finance, a replicating portfolio for a given asset or series of cash flows is a portfolio of assets with the same properties. This is meant in two distinct senses: static replication, where the portfolio has the same cash flows as the reference asset, and dynamic replication, where the portfolio does not have the same cash flows, but has the same "Greeks" as the reference asset, meaning that for small changes to underlying market parameters, the price of the asset and the price of the portfolio change in the same way. Dynamic replication requires continual adjustment, as the asset and portfolio are only assumed to behave similarly at a single point.
