Related Research Articles

Chaos theory is an interdisciplinary scientific theory and branch of mathematics focused on underlying patterns and deterministic laws, of dynamical systems, that are highly sensitive to initial conditions, that were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.

In mathematics, specifically bifurcation theory, the Feigenbaum constants are two mathematical constants which both express ratios in a bifurcation diagram for a non-linear map. They are named after the physicist Mitchell J. Feigenbaum.
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.

In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with initial separation vector diverge at a rate given by

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.
Mathematical and theoretical biology, or biomathematics, is a branch of biology which employs theoretical analysis, mathematical models and abstractions of the living organisms to investigate the principles that govern the structure, development and behavior of the systems, as opposed to experimental biology which deals with the conduction of experiments to prove and validate the scientific theories. The field is sometimes called mathematical biology or biomathematics to stress the mathematical side, or theoretical biology to stress the biological side. Theoretical biology focuses more on the development of theoretical principles for biology while mathematical biology focuses on the use of mathematical tools to study biological systems, even though the two terms are sometimes interchanged.
In the study of dynamical systems, a delay embedding theorem gives the conditions under which a chaotic dynamical system can be reconstructed from a sequence of observations of the state of a dynamical system. The reconstruction preserves the properties of the dynamical system that do not change under smooth coordinate changes, but it does not preserve the geometric shape of structures in phase space.
In mathematics, the replicator equation is a deterministic monotone non-linear and non-innovative game dynamic used in evolutionary game theory. The replicator equation differs from other equations used to model replication, such as the quasispecies equation, in that it allows the fitness function to incorporate the distribution of the population types rather than setting the fitness of a particular type constant. This important property allows the replicator equation to capture the essence of selection. Unlike the quasispecies equation, the replicator equation does not incorporate mutation and so is not able to innovate new types or pure strategies.

Dynamical systems theory is an area of mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.

The Rabinovich–Fabrikant equations are a set of three coupled ordinary differential equations exhibiting chaotic behaviour for certain values of the parameters. They are named after Mikhail Rabinovich and Anatoly Fabrikant, who described them in 1979.

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems and discrete systems.

Schröder's equation, named after Ernst Schröder, is a functional equation with one independent variable: given the function h, find the function Ψ such that
Systems immunology is a research field under systems biology that uses mathematical approaches and computational methods to examine the interactions within cellular and molecular networks of the immune system. The immune system has been thoroughly analyzed as regards to its components and function by using a "reductionist" approach, but its overall function can't be easily predicted by studying the characteristics of its isolated components because they strongly rely on the interactions among these numerous constituents. It focuses on in silico experiments rather than in vivo.

A Boolean network consists of a discrete set of boolean variables each of which has a Boolean function assigned to it which takes inputs from a subset of those variables and output that determines the state of the variable it is assigned to. This set of functions in effect determines a topology (connectivity) on the set of variables, which then become nodes in a network. Usually, the dynamics of the system is taken as a discrete time series where the state of the entire network at time t+1 is determined by evaluating each variable's function on the state of the network at time t. This may be done synchronously or asynchronously.
Reservoir computing is a framework for computation derived from recurrent neural network theory that maps input signals into higher dimensional computational spaces through the dynamics of a fixed, non-linear system called a reservoir. After the input signal is fed into the reservoir, which is treated as a "black box," a simple readout mechanism is trained to read the state of the reservoir and map it to the desired output. The first key benefit of this framework is that training is performed only at the readout stage, as the reservoir dynamics are fixed. The second is that the computational power of naturally available systems, both classical and quantum mechanical, can be used to reduce the effective computational cost.
A coupled map lattice (CML) is a dynamical system that models the behavior of non-linear systems. They are predominantly used to qualitatively study the chaotic dynamics of spatially extended systems. This includes the dynamics of spatiotemporal chaos where the number of effective degrees of freedom diverges as the size of the system increases.
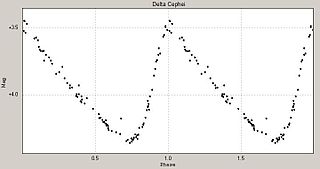
Stellar pulsations are caused by expansions and contractions in the outer layers as a star seeks to maintain equilibrium. These fluctuations in stellar radius cause corresponding changes in the luminosity of the star. Astronomers are able to deduce this mechanism by measuring the spectrum and observing the Doppler effect. Many intrinsic variable stars that pulsate with large amplitudes, such as the classical Cepheids, RR Lyrae stars and large-amplitude Delta Scuti stars show regular light curves.
Microscale models form a broad class of computational models that simulate fine-scale details, in contrast with macroscale models, which amalgamate details into select categories. Microscale and macroscale models can be used together to understand different aspects of the same problem.
Michael Ghil is an American and European mathematician and physicist, focusing on the climate sciences and their interdisciplinary aspects. He is a founder of theoretical climate dynamics, as well as of advanced data assimilation methodology. He has systematically applied dynamical systems theory to planetary-scale flows, both atmospheric and oceanic. Ghil has used these methods to proceed from simple flows with high temporal regularity and spatial symmetry to the observed flows, with their complex behavior in space and time. His studies of climate variability on many time scales have used a full hierarchy of models, from the simplest ‘toy’ models all the way to atmospheric, oceanic and coupled general circulation models. Recently, Ghil has also worked on modeling and data analysis in population dynamics, macroeconomics, and the climate–economy–biosphere system.
References
- ↑ Cavalcante, Hugo L. D. de S.; Gauthier, Daniel J.; Socolar, Joshua E. S.; Zhang, Rui (2010). "On the origin of chaos in autonomous Boolean networks". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 368 (1911): 495–513. arXiv: 0909.2269 . Bibcode:2010RSPTA.368..495C. doi:10.1098/rsta.2009.0235. ISSN 1364-503X. PMID 20008414. S2CID 426841.