In quantum mechanics, bra–ket notation, or Dirac notation, is ubiquitous. The notation uses the angle brackets, "" and "", and a vertical bar "", to construct "bras" and "kets". A ket looks like "". Mathematically it denotes a vector, , in an abstract (complex) vector space , and physically it represents a state of some quantum system. A bra looks like "", and mathematically it denotes a linear form , i.e. a linear map that maps each vector in to a number in the complex plane . Letting the linear functional act on a vector is written as .

In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams in 1948. The interaction of subatomic particles can be complex and difficult to understand; Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory. Frank Wilczek wrote that the calculations which won him the 2004 Nobel Prize in Physics "would have been literally unthinkable without Feynman diagrams, as would [Wilczek's] calculations that established a route to production and observation of the Higgs particle."
A density matrix is a matrix that describes the statistical state, whether pure or mixed, of a system in quantum mechanics. The probability for any outcome of any well-defined measurement upon a system can be calculated from the density matrix for that system. The extreme points in the set of density matrices are the pure states, which can also be written as state vectors or wavefunctions. Density matrices that are not pure states are mixed states. Any mixed state can be represented as a convex combination of pure states, and so density matrices are helpful for dealing with statistical ensembles of different possible preparations of a quantum system, or situations where a precise preparation is not known, as in quantum statistical mechanics.
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the best known mathematical approximation in molecular dynamics. Specifically, it is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. The approach is named after Max Born and J. Robert Oppenheimer who proposed it in 1927, in the early period of quantum mechanics.
In quantum mechanics, wave function collapse occurs when a wave function—initially in a superposition of several eigenstates—reduces to a single eigenstate due to interaction with the external world. This interaction is called an "observation". It is the essence of a measurement in quantum mechanics which connects the wave function with classical observables like position and momentum. Collapse is one of two processes by which quantum systems evolve in time; the other is the continuous evolution via the Schrödinger equation. Collapse is a black box for a thermodynamically irreversible interaction with a classical environment. Calculations of quantum decoherence show that when a quantum system interacts with the environment, the superpositions apparently reduce to mixtures of classical alternatives. Significantly, the combined wave function of the system and environment continue to obey the Schrödinger equation. More importantly, this is not enough to explain wave function collapse, as decoherence does not reduce it to a single eigenstate.

A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it. The most common symbols for a wave function are the Greek letters ψ and Ψ.

Quantum decoherence is the loss of quantum coherence. In quantum mechanics, particles such as electrons are described by a wave function, a mathematical representation of the quantum state of a system; a probabilistic interpretation of the wave function is used to explain various quantum effects. As long as there exists a definite phase relation between different states, the system is said to be coherent. A definite phase relationship is necessary to perform quantum computing on quantum information encoded in quantum states. Coherence is preserved under the laws of quantum physics.
The Klein–Gordon equation is a relativistic wave equation, related to the Schrödinger equation. It is second-order in space and time and manifestly Lorentz-covariant. It is a quantized version of the relativistic energy–momentum relation. Its solutions include a quantum scalar or pseudoscalar field, a field whose quanta are spinless particles. Its theoretical relevance is similar to that of the Dirac equation. Electromagnetic interactions can be incorporated, forming the topic of scalar electrodynamics, but because common spinless particles like the pions are unstable and also experience the strong interaction the practical utility is limited.
In quantum mechanics, the spin–statistics theorem relates the intrinsic spin of a particle to the particle statistics it obeys. In units of the reduced Planck constant ħ, all particles that move in 3 dimensions have either integer spin or half-integer spin.
Coupled cluster (CC) is a numerical technique used for describing many-body systems. Its most common use is as one of several post-Hartree–Fock ab initio quantum chemistry methods in the field of computational chemistry, but it is also used in nuclear physics. Coupled cluster essentially takes the basic Hartree–Fock molecular orbital method and constructs multi-electron wavefunctions using the exponential cluster operator to account for electron correlation. Some of the most accurate calculations for small to medium-sized molecules use this method.

The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to the presence of an external electric field. It is the electric-field analogue of the Zeeman effect, where a spectral line is split into several components due to the presence of the magnetic field. Although initially coined for the static case, it is also used in the wider context to describe the effect of time-dependent electric fields. In particular, the Stark effect is responsible for the pressure broadening of spectral lines by charged particles in plasmas. For most spectral lines, the Stark effect is either linear or quadratic with a high accuracy.
In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).

The Schwinger–Dyson equations (SDEs), or Dyson–Schwinger equations, named after Julian Schwinger and Freeman Dyson, are general relations between Green functions in quantum field theories (QFTs). They are also referred to as the Euler–Lagrange equations of quantum field theories, since they are the equations of motion corresponding to the Green's function.
Generally in scattering theory and in particular in quantum mechanics, the Born approximation consists of taking the incident field in place of the total field as the driving field at each point in the scatterer. The Born approximation is named after Max Born who proposed this approximation in early days of quantum theory development.
The Lippmann–Schwinger equation is one of the most used equations to describe particle collisions – or, more precisely, scattering – in quantum mechanics. It may be used in scattering of molecules, atoms, neutrons, photons or any other particles and is important mainly in atomic, molecular, and optical physics, nuclear physics and particle physics, but also for seismic scattering problems in geophysics. It relates the scattered wave function with the interaction that produces the scattering and therefore allows calculation of the relevant experimental parameters.
Schwinger variational principle is a variational principle which expresses the scattering T-matrix as a functional depending on two unknown wave functions. The functional attains stationary value equal to actual scattering T-matrix. The functional is stationary if and only if the two functions satisfy the Lippmann-Schwinger equation. The development of the variational formulation of the scattering theory can be traced to works of L. Hultén and J. Schwinger in 1940s.
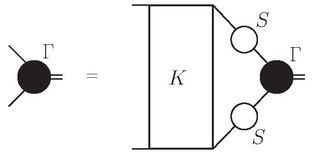
The Bethe–Salpeter equation describes the bound states of a two-body (particles) quantum field theoretical system in a relativistically covariant formalism. The equation was actually first published in 1950 at the end of a paper by Yoichiro Nambu, but without derivation.
In quantum physics, unitarity is the condition that the time evolution of a quantum state according to the Schrödinger equation is mathematically represented by a unitary operator. This is typically taken as an axiom or basic postulate of quantum mechanics, while generalizations of or departures from unitarity are part of speculations about theories that may go beyond quantum mechanics. A unitarity bound is any inequality that follows from the unitarity of the evolution operator, i.e. from the statement that time evolution preserves inner products in Hilbert space.
The method of continued fractions is a method developed specifically for solution of integral equations of quantum scattering theory like Lippmann-Schwinger equation or Faddeev equations. It was invented by Horáček and Sasakawa in 1983. The goal of the method is to solve the integral equation
Multiple scattering theory (MST) is the mathematical formalism that is used to describe the propagation of a wave through a collection of scatterers. Examples are acoustical waves traveling through porous media, light scattering from water droplets in a cloud, or x-rays scattering from a crystal. A more recent application is to the propagation of quantum matter waves like electrons or neutrons through a solid.























