In mathematics, a Catanese surface is one of the surfaces of general type introduced by Catanese (1981).
The construction starts with a quintic V with 20 double points. Let W be the surface obtained by blowing up the 20 double points. Suppose that W has a double cover X branched over the 20 exceptional −2-curves. Let Y be obtained from X by blowing down the 20 −1-curves in X. If there is a group of order 5 acting freely on all these surfaces, then the quotient Z of Y by this group of order 5 is a Catanese surface. Catanese found a 4-dimensional family of curves constructed like this.
The Catanese surface is a numerical Campedelli surface and hence has Hodge diamond
In mathematics, a Campedelli surface is one of the surfaces of general type introduced by Campedelli. Surfaces with the same Hodge numbers are called numerical Campedelli surfaces.
| 1 | ||||
| 0 | 0 | |||
| 0 | 8 | 0 | ||
| 0 | 0 | |||
| 1 |
and canonical degree . The fundamental group of the Catanese surface is , as can be seen from its quotient construction.
In mathematics, an elliptic curve is a plane algebraic curve defined by an equation of the form
In mathematics, curvature is any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object such as a surface deviates from being a flat plane, or a curve from being straight as in the case of a line, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space – in a way that relates to the radius of curvature of circles that touch the object – and intrinsic curvature, which is defined in terms of the lengths of curves within a Riemannian manifold.
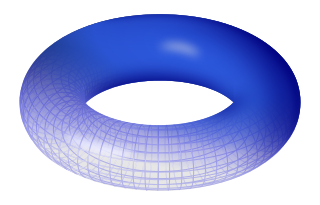
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space about an axis coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution.
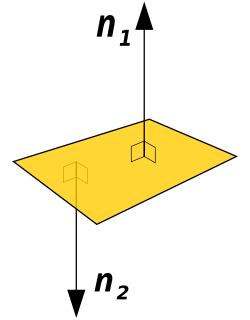
In geometry, a normal is an object such as a line or vector that is perpendicular to a given object. For example, in two dimensions, the normal line to a curve at a given point is the line perpendicular to the tangent line to the curve at the point.
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" (cosets) of H that fill up G. For example, if H has index 2 in G, then intuitively half of the elements of G lie in H. The index of H in G is usually denoted |G : H| or [G : H] or (G:H).
Algebraic varieties are the central objects of study in algebraic geometry. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional plane σp in the tangent space at a point p of the manifold. It is the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a smooth real-valued function on the 2-Grassmannian bundle over the manifold.
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P(V). Explicitly, the projective linear group is the quotient group
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in R3 passing through the origin.
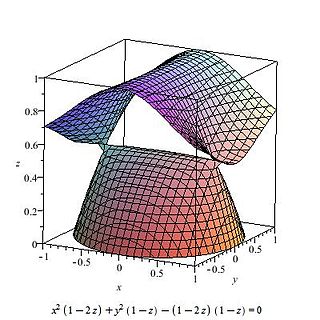
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single quaternary cubic polynomial which is homogeneous of degree 3. Cubic surfaces are del Pezzo surfaces.
In algebraic geometry, a Kummer quartic surface, first studied by Kummer (1864), is an irreducible nodal surface of degree 4 in with the maximal possible number of 16 double points. Any such surface is the Kummer variety of the Jacobian variety of a smooth hyperelliptic curve of genus 2; i.e. a quotient of the Jacobian by the Kummer involution x ↦ −x. The Kummer involution has 16 fixed points: the 16 2-torsion point of the Jacobian, and they are the 16 singular points of the quartic surface. Resolving the 16 double points of the quotient of a torus by the Kummer involution gives a K3 surface with 16 disjoint rational curves; these K3 surfaces are also sometimes called Kummer surfaces.
In number theory and algebraic geometry, a modular curveY(Γ) is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL(2, Z). The term modular curve can also be used to refer to the compactified modular curvesX(Γ) which are compactifications obtained by adding finitely many points to this quotient. The points of a modular curve parametrize isomorphism classes of elliptic curves, together with some additional structure depending on the group Γ. This interpretation allows one to give a purely algebraic definition of modular curves, without reference to complex numbers, and, moreover, prove that modular curves are defined either over the field Q of rational numbers, or a cyclotomic field. The latter fact and its generalizations are of fundamental importance in number theory.
In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group . These concepts are named after the mathematician J. H. C. Whitehead.
In mathematics, in the sub-field of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
In mathematics, real projective space, or RPn or , is the topological space of lines passing through the origin 0 in Rn+1. It is a compact, smooth manifold of dimension n, and is a special case Gr(1, Rn+1) of a Grassmannian space.
In mathematics, Hurwitz's automorphisms theorem bounds the order of the group of automorphisms, via orientation-preserving conformal mappings, of a compact Riemann surface of genus g > 1, stating that the number of such automorphisms cannot exceed 84(g − 1). A group for which the maximum is achieved is called a Hurwitz group, and the corresponding Riemann surface a Hurwitz surface. Because compact Riemann surfaces are synonymous with non-singular complex projective algebraic curves, a Hurwitz surface can also be called a Hurwitz curve. The theorem is named after Adolf Hurwitz, who proved it in.
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point. The metaphor is that of zooming in on a photograph to enlarge part of the picture, rather than referring to an explosion.
Three-dimensional space is a geometric setting in which three values are required to determine the position of an element. This is the informal meaning of the term dimension.
In algebraic geometry, the Chow groups of an algebraic variety over any field are algebro-geometric analogs of the homology of a topological space. The elements of the Chow group are formed out of subvarieties in a similar way to how simplicial or cellular homology groups are formed out of subcomplexes. When the variety is smooth, the Chow groups can be interpreted as cohomology groups and have a multiplication called the intersection product. The Chow groups carry rich information about an algebraic variety, and they are correspondingly hard to compute in general.
This is a glossary of algebraic geometry.
The International Standard Book Number (ISBN) is a numeric commercial book identifier which is intended to be unique. Publishers purchase ISBNs from an affiliate of the International ISBN Agency.
Mathematical Reviews is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also publishes an associated online bibliographic database called MathSciNet which contains an electronic version of Mathematical Reviews and additionally contains citation information for over 3.5 million items as of 2018.
