In probability theory, de Finetti's theorem states that exchangeable observations are conditionally independent relative to some latent variable. An epistemic probability distribution could then be assigned to this variable. It is named in honor of Bruno de Finetti.
The following outline is provided as an overview of and guide to category theory, the area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows, where these collections satisfy certain basic conditions. Many significant areas of mathematics can be formalised as categories, and the use of category theory allows many intricate and subtle mathematical results in these fields to be stated, and proved, in a much simpler way than without the use of categories.
In category theory, a branch of mathematics, a monad is a triple consisting of a functor T from a category to itself and two natural transformations that satisfy the conditions like associativity. For example, if are functors adjoint to each other, then together with determined by the adjoint relation is a monad.
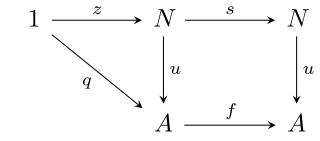
In category theory, a natural numbers object (NNO) is an object endowed with a recursive structure similar to natural numbers. More precisely, in a category E with a terminal object 1, an NNO N is given by:
- a global element z : 1 → N, and
- an arrow s : N → N,
In mathematics, categorification is the process of replacing set-theoretic theorems with category-theoretic analogues. Categorification, when done successfully, replaces sets with categories, functions with functors, and equations with natural isomorphisms of functors satisfying additional properties. The term was coined by Louis Crane.
This is a glossary of properties and concepts in category theory in mathematics.
In category theory, a branch of mathematics, for every object in every category where the product exists, there exists the diagonal morphism
In category theory, a Lawvere theory is a category that can be considered a categorical counterpart of the notion of an equational theory.
Isbell conjugacy is a fundamental construction of enriched category theory formally introduced by William Lawvere in 1986. That is a duality between covariant and contravariant representable presheaves associated with an objects of categories under the Yoneda embedding. In addition, Lawvere is states as follows; "Then the conjugacies are the first step toward expressing the duality between space and quantity fundamental to mathematics".

Ronald Brown FLSW is an English mathematician. Emeritus Professor in the School of Computer Science at Bangor University, he has authored many books and more than 160 journal articles.
In mathematics, a categorical ring is, roughly, a category equipped with addition and multiplication. In other words, a categorical ring is obtained by replacing the underlying set of a ring by a category. For example, given a ring R, let C be a category whose objects are the elements of the set R and whose morphisms are only the identity morphisms. Then C is a categorical ring. But the point is that one can also consider the situation in which an element of R comes with a "nontrivial automorphism".
Higher Topos Theory is a treatise on the theory of ∞-categories written by American mathematician Jacob Lurie. In addition to introducing Lurie's new theory of ∞-topoi, the book is widely considered foundational to higher category theory. Since 2018, Lurie has been transferring the contents of Higher Topos Theory to Kerodon, an "online resource for homotopy-coherent mathematics" inspired by the Stacks Project.
In algebra, given a 2-monad T in a 2-category, a pseudoalgebra for T is a 2-category-version of algebra for T, that satisfies the laws up to coherent isomorphisms.
In mathematics, nonabelian algebraic topology studies an aspect of algebraic topology that involves higher-dimensional algebras.
In mathematics, the category of measurable spaces, often denoted Meas, is the category whose objects are measurable spaces and whose morphisms are measurable maps. This is a category because the composition of two measurable maps is again measurable, and the identity function is measurable.
In mathematics, the category of Markov kernels, often denoted Stoch, is the category whose objects are measurable spaces and whose morphisms are Markov kernels. It is analogous to the category of sets and functions, but where the arrows can be interpreted as being stochastic.
In mathematics, the Giry monad is a construction that assigns to a measurable space a space of probability measures over it, equipped with a canonical sigma-algebra. It is one of the main examples of a probability monad.
In mathematics, especially in topology, a pyknotic set is a sheaf of sets on the site of compact Hausdorff spaces. The notion was introduced by Barwick and Haine to provide a convenient setting for homological algebra. The term pyknotic comes from the Greek πυκνός, meaning dense, compact or thick. The notion can be compared to other approaches of introducing generalized spaces for the purpose of homological algebra such as Clausen and Scholze‘s condensed sets or Johnstone‘s topological topos.
In mathematics, specifically in category theory, a generalized metric space is a metric space but without the symmetry property and some other properties. Precisely, it is a category enriched over , the one-point compactification of . The notion was introduced in 1973 by Lawvere who noticed that a metric space can be viewed as a particular kind of a category.
In mathematics, the Elementary Theory of the Category of Sets or ETCS is a set of axioms for set theory proposed by William Lawvere. Although it was originally stated in the language of category theory, as Leinster pointed out, the axioms can be stated without references to category theory.

