In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles Catalan (1814–1894).

Arthur Cayley was a prolific British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics.

In combinatorics, a branch of mathematics, the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; symbolically expressed as

In mathematics, the double factorial or semifactorial of a number n, denoted by n‼, is the product of all the integers from 1 up to n that have the same parity as n. That is,

In mathematics, Cayley's formula is a result in graph theory named after Arthur Cayley. It states that for every positive integer , the number of trees on labeled vertices is .
Latin squares and quasigroups are equivalent mathematical objects, although the former has a combinatorial nature while the latter is more algebraic. The listing below will consider the examples of some very small orders, which is the side length of the square, or the number of elements in the equivalent quasigroup.
In the game of bridge mathematical probabilities play a significant role. Different declarer play strategies lead to success depending on the distribution of opponent's cards. To decide which strategy has highest likelihood of success, the declarer needs to have at least an elementary knowledge of probabilities.

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the number of weak orderings on a set of n elements. Starting from n = 0, these numbers are

In combinatorics, an area of mathematics, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graphs of certain types, typically as a function of the number of vertices of the graph. These problems may be solved either exactly or asymptotically. The pioneers in this area of mathematics were George Pólya, Arthur Cayley and J. Howard Redfield.
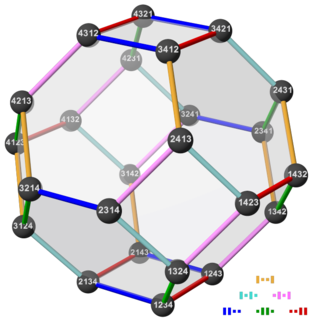
In mathematics, the permutohedron of order n is an (n − 1)-dimensional polytope embedded in an n-dimensional space. Its vertex coordinates (labels) are the permutations of the first n natural numbers. The edges identify the shortest possible paths that connect two vertices (permutations). Two permutations connected by an edge differ in only two places, and the numbers on these places are neighbors.
The mathematical field of combinatorics was studied to varying degrees in numerous ancient societies. Its study in Europe dates to the work of Leonardo Fibonacci in the 13th century AD, which introduced Arabian and Indian ideas to the continent. It has continued to be studied in the modern era.

In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of male-female couples at a round dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas and independently, a few years earlier, by Peter Guthrie Tait in connection with knot theory. For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is

In computer science and discrete mathematics, an inversion in a sequence is a pair of elements that are out of their natural order.
In combinatorial mathematics and theoretical computer science, a permutation pattern is a sub-permutation of a longer permutation. Any permutation may be written in one-line notation as a sequence of digits representing the result of applying the permutation to the digit sequence 123...; for instance the digit sequence 213 represents the permutation on three elements that swaps elements 1 and 2. If π and σ are two permutations represented in this way, then π is said to contain σ as a pattern if some subsequence of the digits of π has the same relative order as all of the digits of σ.
In combinatorial mathematics, a partial permutation, or sequence without repetition, on a finite set S is a bijection between two specified subsets of S. That is, it is defined by two subsets U and V of equal size, and a one-to-one mapping from U to V. Equivalently, it is a partial function on S that can be extended to a permutation.
A Gilbreath shuffle is a way to shuffle a deck of cards, named after mathematician Norman Gilbreath. Gilbreath's principle describes the properties of a deck that are preserved by this type of shuffle, and a Gilbreath permutation is a permutation that can be formed by a Gilbreath shuffle.
In the mathematics of shuffling playing cards, the Gilbert–Shannon–Reeds model is a probability distribution on riffle shuffle permutations that has been reported to be a good match for experimentally observed outcomes of human shuffling, and that forms the basis for a recommendation that a deck of cards should be riffled seven times in order to thoroughly randomize it. It is named after the work of Edgar Gilbert, Claude Shannon, and J. Reeds, reported in a 1955 technical report by Gilbert and in a 1981 unpublished manuscript of Reeds.
In the mathematics of permutations, a layered permutation is a permutation that reverses contiguous blocks of elements. Equivalently, it is the direct sum of decreasing permutations.












