Cell Transmission Model

Last updated

Cell Transmission Model (CTM) is a popular numerical method proposed by Carlos Daganzo [1] to solve the kinematic wave equation. [2] [3] Lebacque [4] later showed that CTM is the first order discrete Godunov approximation. [5]

Contents

Background

CTM predicts macroscopic traffic behavior on a given corridor by evaluating the flow and density at finite number of intermediate points at different time steps. This is done by dividing the corridor into homogeneous sections (hereafter called cells) and numbering them i=1, 2… n starting downstream. The length of the cell is chosen such that it is equal to the distance traveled by free-flow traffic in one evaluation time step. The traffic behavior is evaluated every time step starting at t=1,2…m. Initial and boundary conditions are required to iteratively evaluate each cell.

The flow across the cells is determined based on μ(k) and λ(k), two monotonic functions that uniquely define the fundamental diagram as shown in Figure 1. The density of the cells is updated based on the conservation of inflows and outflows. Thus, the flow and density are derived as:

Where:

 and represent density and flow in cell i at time t. Similarly $f_k$, , ,and  represents jam density,  capacity, wave speed, and free-flow speed respectively of the fundamental diagram.

CTM produces results consistent with the continuous Kinematic wave equation when the density specified in the initial condition changes gradually. However, CTM replicates discontinuities and shock that take a span of few cells of space but moves at correct speed predicted by the Kinematic wave equation.

It was observed that as time passes, the CTM approximations result in spreading the shock to a growing number of cells. To eliminate spreading of certain shocks, Daganzo (1994) proposed a modification to the CTM that ensures shocks separating a lower upstream density and greater downstream density do not spread.

CTM is robust and the simulation results do not depend on the order in which the cells are evaluated because the flow entering a cell is dependent only on the current conditions within the cell and is unrelated to the flow exiting the cell. Thus, CTM can be applied for the analysis of complex networks and non-concave fundamental diagrams.

Implementation and Example

Consider a 2.5 kilometer homogeneous arterial segment that follows a triangular fundamental diagram as shown in figure 2.

Figure 2. Fundamental diagram for the example

This corridor is divided into 30 cells and is simulated for 480 seconds with a time step of 6 seconds. The Initial and boundary conditions are specified as follows: K(x,0)=48 x K(0,t)=48 t K(2.5,t)=0 t

The corridor has two signals located at milepost 1 and 2 starting upstream. The signals have a split of 30 seconds and a cycle length of 60 second. With this information, it is a simple matter of iteration of equations (1) for all the cells and time steps. Figure 3 and Table 1 shows the spatial and temporal distribution of density for the case of offset=0 seconds.

Table 1: Density values for the example with offset of 0 seconds

Currently, some software tools (For example: TRANSYT-14 and SIGMIX) evaluating traffic or optimizing traffic signal settings applies CTM as its macroscopic traffic simulator. For example, in TRANSYT-14 (Note not to be confused with TRANSYT-7F releases), the user is allowed to choose traffic models including CTM, Platoon Dispersion...etc. to model the traffic dynamics. [7] In SIGMIX, it is by default using CTM as simulator. [8]

Lagged Cell Transmission Model

Since the original Cell Transmission model is a first order approximation, Daganzo [9] proposed the Lagged Cell Transmission Model (LCTM) that is more accurate than the former. This enhanced model uses lagged downstream density (p time steps earlier than the current time) for the receiving function. If a triangular fundamental diagram is used and lag is chosen appropriately, this improved method is second order accurate.

when the highway is discritized with variable cell lengths, then one should introduce forward lag for the sending function to preserve the good properties of LCTM. The choice of backward lag and forward lag are given by:

backward lag forward lag

where d and ε are the spatial and temporal steps of the cell, is the maximum free-flow speed, w is the maximum backward propagating wave speed.

Newell’s Exact Method

Newell [10] proposed an exact method to solve the kinematic wave equation based on cumulative curves only at either ends of the corridor, without evaluating any intermediate points.

Since the density is constant along the characteristics, if one knows the cumulative curves A(x0,t0) and flow q(x0,t0) at boundary, one can construct the three-dimensional surface (A,x,t). However, if characteristics intersect, the surface is a multi-valued function of x,t based on the initial and boundary conditions it is derived from. In such a case, a unique and continuous solution is obtained by taking the lower envelope of the multi-valued solution derived based on different boundary and initial conditions.

However, the limitation of this method is that it can not be used for non-concave fundamental diagrams.

Newell proposed the method, but Daganzo [11] using variational theory proved that the lower envelope is the unique solution.

Related Research Articles

<span class="mw-page-title-main">Aerodynamics</span> Branch of dynamics concerned with studying the motion of air

Aerodynamics is the study of the motion of air, particularly when affected by a solid object, such as an airplane wing. It involves topics covered in the field of fluid dynamics and its subfield of gas dynamics, and is an important domain of study in aeronautics. The term aerodynamics is often used synonymously with gas dynamics, the difference being that "gas dynamics" applies to the study of the motion of all gases, and is not limited to air. The formal study of aerodynamics began in the modern sense in the eighteenth century, although observations of fundamental concepts such as aerodynamic drag were recorded much earlier. Most of the early efforts in aerodynamics were directed toward achieving heavier-than-air flight, which was first demonstrated by Otto Lilienthal in 1891. Since then, the use of aerodynamics through mathematical analysis, empirical approximations, wind tunnel experimentation, and computer simulations has formed a rational basis for the development of heavier-than-air flight and a number of other technologies. Recent work in aerodynamics has focused on issues related to compressible flow, turbulence, and boundary layers and has become increasingly computational in nature.

<span class="mw-page-title-main">Fluid dynamics</span> Aspects of fluid mechanics involving flow

In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including aerodynamics and hydrodynamics. Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation.

<span class="mw-page-title-main">Wave</span> Repeated oscillation around equilibrium

In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance of one or more quantities. Periodic waves oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a travelling wave; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a standing wave. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. Waves are often described by a wave equation or a one-way wave equation for single wave propagation in a defined direction.

<span class="mw-page-title-main">Shock wave</span> Propagating disturbance

In physics, a shock wave, or shock, is a type of propagating disturbance that moves faster than the local speed of sound in the medium. Like an ordinary wave, a shock wave carries energy and can propagate through a medium but is characterized by an abrupt, nearly discontinuous, change in pressure, temperature, and density of the medium.

Compressible flow is the branch of fluid mechanics that deals with flows having significant changes in fluid density. While all flows are compressible, flows are usually treated as being incompressible when the Mach number is smaller than 0.3. The study of compressible flow is relevant to high-speed aircraft, jet engines, rocket motors, high-speed entry into a planetary atmosphere, gas pipelines, commercial applications such as abrasive blasting, and many other fields.

<span class="mw-page-title-main">Transonic</span> Flight condition in which airflow speeds are concurrently above and below the speed of sound

Transonic flow is air flowing around an object at a speed that generates regions of both subsonic and supersonic airflow around that object. The exact range of speeds depends on the object's critical Mach number, but transonic flow is seen at flight speeds close to the speed of sound, typically between Mach 0.8 and 1.2.

<span class="mw-page-title-main">Computational fluid dynamics</span> Analysis and solving of problems that involve fluid flows

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.

Traffic waves, also called stop waves, ghost jams, traffic snakes or traffic shocks, are traveling disturbances in the distribution of cars on a highway. Traffic waves travel backwards relative to the cars themselves. Relative to a fixed spot on the road the wave can move with, or against the traffic, or even be stationary. Traffic waves are a type of traffic jam. A deeper understanding of traffic waves is a goal of the physical study of traffic flow, in which traffic itself can often be seen using techniques similar to those used in fluid dynamics. It is related to the accordion effect.

Fluid mechanics is the branch of physics concerned with the mechanics of fluids and the forces on them. It has applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical, and biomedical engineering, as well as geophysics, oceanography, meteorology, astrophysics, and biology.

In transportation engineering, traffic flow is the study of interactions between travellers and infrastructure, with the aim of understanding and developing an optimal transport network with efficient movement of traffic and minimal traffic congestion problems.

<span class="mw-page-title-main">Fundamental diagram of traffic flow</span> Type of diagram

The fundamental diagram of traffic flow is a diagram that gives a relation between road traffic flux (vehicles/hour) and the traffic density (vehicles/km). A macroscopic traffic model involving traffic flux, traffic density and velocity forms the basis of the fundamental diagram. It can be used to predict the capability of a road system, or its behaviour when applying inflow regulation or speed limits.

In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.

<span class="mw-page-title-main">Traffic bottleneck</span> Localized disruption of vehicular traffic on a street, road, or highway

A traffic bottleneck is a localized disruption of vehicular traffic on a street, road, or highway. As opposed to a traffic jam, a bottleneck is a result of a specific physical condition, often the design of the road, badly timed traffic lights, or sharp curves. They can also be caused by temporary situations, such as vehicular accidents.

In traffic flow theory, Newell’s car-following model is a method used to determine how vehicles follow one another on a roadway. The main idea of this model is that a vehicle will maintain a minimum space and time gap between it and the vehicle that precedes it. Thus, under congested conditions, if the leading car changes its speed, the following vehicle will also change speed at a point in time-space along the traffic wave speed, -w.

The Three-detector problem is a problem in traffic flow theory. Given is a homogeneous freeway and the vehicle counts at two detector stations. We seek the vehicle counts at some intermediate location. The method can be applied to incident detection and diagnosis by comparing the observed and predicted data, so a realistic solution to this problem is important. Newell G.F. proposed a simple method to solve this problem. In Newell's method, one gets the cumulative count curve (N-curve) of any intermediate location just by shifting the N-curves of the upstream and downstream detectors. Newell's method was developed before the variational theory of traffic flow was proposed to deal systematically with vehicle counts. This article shows how Newell's method fits in the context of variational theory.

A macroscopic traffic flow model is a mathematical traffic model that formulates the relationships among traffic flow characteristics like density, flow, mean speed of a traffic stream, etc.. Such models are conventionally arrived at by integrating microscopic traffic flow models and converting the single-entity level characteristics to comparable system level characteristics. An example is the two-fluid model.

<span class="mw-page-title-main">Newell–Daganzo merge model</span>

In traffic flow theory, the Newell–Daganzo merge model describes a simple procedure on how to determine the flows exiting two branch roadways and merging to flow through a single roadway. The model is simple in that it does not consider the actual merging process between vehicles as the two branch roadways come together. The only information required to calculate the flows leaving the two branch roadways are the capacities of the two branch roadways and the exiting capacity, the demands into the system, and a value describing how the two input flows interact. This latter input term is called the split priority, or merge ratio, and is defined as the proportion of the two input flows when both are operating in congested conditions.

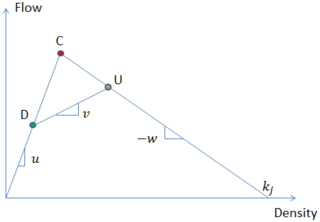
<span class="mw-page-title-main">Truck lane restriction</span>

Truck lane restriction within transportation traffic engineering, is a factor impacting freeway truck lanes and traffic congestion. In traffic flow theory, intuitively, slow vehicles will cause queues behind them, but how it relates to the kinematic wave theory was not revealed until Newell. Leclercq et al did a complete review of Newell's theory. In addition to the simulation models developed by Laval and Daganzo on the basis of numerical solution methods for Newell's theory to capture the impacts of slow vehicle, Laval also mathematically derived the analytical capacity formulas for bottlenecks caused by single-type of trucks for multi-lane freeway segments.

In gravity and pressure driven fluid dynamical and geophysical mass flows such as ocean waves, avalanches, debris flows, mud flows, flash floods, etc., kinematic waves are important mathematical tools to understand the basic features of the associated wave phenomena. These waves are also applied to model the motion of highway traffic flows.

The index of physics articles is split into multiple pages due to its size.

References

  1. ↑ Daganzo C.F., The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory, Transportation Research Part B: Methodological, Volume 28, Issue 4, August 1994, Pages 269-287
  2. ↑ Lighthill and Witham, On kinematic waves: II. A theory of traffic flow on long crowded roads. Proceedings of the Royal Society of London (Series A). 229(1178). pp. 317-345, 1955
  3. ↑ Richards, Shock waves on the Highway. Operations Research. 4(1). pp. 42-51, 1956
  4. ↑ Lebacque, The godunov scheme and what it means for first order traffic flow models. In J. B. Lesort, editor, 13th ISTTT Symposium, pages 647–678, Elsevier, New York, 1996
  5. ↑ Godunov, A Difference Scheme for Numerical Solution of Discontinuous Solution of Hydrodynamic Equations, Mat. Sbornik, 47, 271-306, 1959
  6. ↑ Laval J. A. Hybrid Models of Traffic Flow: Impacts of Bounded Vehicle Accelerations. Ph.D. dissertation, UC Berkeley, 2004
  7. ↑ Binnings, Crabtree, and Burtenshaw (2010), "Application Guide 65 (Issue E) TRANSYT 14 USER GUIDE", p.33
  8. ↑ Chen (2016), "Guide to mixMIX: the key to optimise traffic signal settings for mixed flow with motorbikes", p.13, Taipei. ISBN   978-986-93619-1-0
  9. ↑ Daganzo C.F. The lagged cell-transmission model, 14th ISTTT Symposium, Jerusalem, Israel, 1999
  10. ↑ Newell G.F. A simplified theory of kinematic waves in highway traffic, part I: General theory, Transportation Research Part B: Methodological, Volume 27, Issue 4, August 1993, Pages 281-287
  11. ↑ Daganzo, C.F. On the Variational Theory of Traffic Flow: Well-Posedness, Duality and Applications. UC Berkeley: UC Berkeley Center for Future Urban Transport: A Volvo Center of Excellence, 2006
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.