
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics. It focuses on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.

Cavitation in fluid mechanics and engineering normally refers to the phenomenon in which the static pressure of a liquid reduces to below the liquid's vapour pressure, leading to the formation of small vapor-filled cavities in the liquid. When subjected to higher pressure, these cavities, called "bubbles" or "voids", collapse and can generate shock waves that may damage machinery. These shock waves are strong when they are very close to the imploded bubble, but rapidly weaken as they propagate away from the implosion. Cavitation is a significant cause of wear in some engineering contexts. Collapsing voids that implode near to a metal surface cause cyclic stress through repeated implosion. This results in surface fatigue of the metal, causing a type of wear also called "cavitation". The most common examples of this kind of wear are to pump impellers, and bends where a sudden change in the direction of liquid occurs. Cavitation is usually divided into two classes of behavior: inertial cavitation and non-inertial cavitation.
In physics, a fluid is a liquid, gas, or other material that may continuously move and deform (flow) under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are substances which cannot resist any shear force applied to them.

Sonoluminescence is the emission of light from imploding bubbles in a liquid when excited by sound.
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.

An antibubble is a droplet of liquid surrounded by a thin film of gas, as opposed to a gas bubble, which is a sphere of gas surrounded by a liquid. Antibubbles are formed when liquid drops or flows turbulently into the same or another liquid. They can either skim across the surface of a liquid such as water, in which case they are also called water globules, or they can be completely submerged into the liquid to which they are directed.

A bubble ring, or toroidal bubble, is an underwater vortex ring where an air bubble occupies the core of the vortex, forming a ring shape. The ring of air as well as the nearby water spins poloidally as it travels through the water, much like a flexible bracelet might spin when it is rolled on to a person's arm. The faster the bubble ring spins, the more stable it becomes. The physics of vortex rings are still under active study in fluid dynamics. Devices have been invented which generate bubble vortex rings.
In dynamical systems theory, a period-doubling bifurcation occurs when a slight change in a system's parameters causes a new periodic trajectory to emerge from an existing periodic trajectory—the new one having double the period of the original. With the doubled period, it takes twice as long for the numerical values visited by the system to repeat themselves.

A bubble is a globule of a gas substance in a liquid. In the opposite case, a globule of a liquid in a gas, is called a drop. Due to the Marangoni effect, bubbles may remain intact when they reach the surface of the immersive substance.
The Richtmyer–Meshkov instability (RMI) occurs when two fluids of different density are impulsively accelerated. Normally this is by the passage of a shock wave. The development of the instability begins with small amplitude perturbations which initially grow linearly with time. This is followed by a nonlinear regime with bubbles appearing in the case of a light fluid penetrating a heavy fluid, and with spikes appearing in the case of a heavy fluid penetrating a light fluid. A chaotic regime eventually is reached and the two fluids mix. This instability can be considered the impulsive-acceleration limit of the Rayleigh–Taylor instability.
In lab experiments that study chaos theory, approaches designed to control chaos are based on certain observed system behaviors. Any chaotic attractor contains an infinite number of unstable, periodic orbits. Chaotic dynamics, then, consists of a motion where the system state moves in the neighborhood of one of these orbits for a while, then falls close to a different unstable, periodic orbit where it remains for a limited time and so forth. This results in a complicated and unpredictable wandering over longer periods of time.
Synchronization of chaos is a phenomenon that may occur when two or more dissipative chaotic systems are coupled.

A bubble column reactor is a chemical reactor that belongs to the general class of multiphase reactors, which consists of three main categories: trickle bed reactor, fluidized bed reactor, and bubble column reactor. A bubble column reactor is a very simple device consisting of a vertical vessel filled with water with a gas distributor at the inlet. Due to the ease of design and operation, which does not involve moving parts, they are widely used in the chemical, biochemical, petrochemical, and pharmaceutical industries to generate and control gas-liquid chemical reactions.
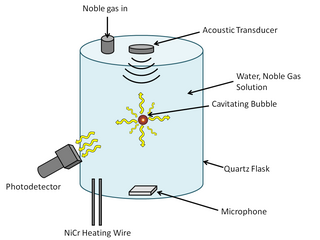
Sonoluminescence is a phenomenon that occurs when a small gas bubble is acoustically suspended and periodically driven in a liquid solution at ultrasonic frequencies, resulting in bubble collapse, cavitation, and light emission. The thermal energy that is released from the bubble collapse is so great that it can cause weak light emission. The mechanism of the light emission remains uncertain, but some of the current theories, which are categorized under either thermal or electrical processes, are Bremsstrahlung radiation, argon rectification hypothesis, and hot spot. Some researchers are beginning to favor thermal process explanations as temperature differences have consistently been observed with different methods of spectral analysis. In order to understand the light emission mechanism, it is important to know what is happening in the bubble's interior and at the bubble's surface.
In the bifurcation theory, a bounded oscillation that is born without loss of stability of stationary set is called a hidden oscillation. In nonlinear control theory, the birth of a hidden oscillation in a time-invariant control system with bounded states means crossing a boundary, in the domain of the parameters, where local stability of the stationary states implies global stability. If a hidden oscillation attracts all nearby oscillations, then it is called a hidden attractor. For a dynamical system with a unique equilibrium point that is globally attractive, the birth of a hidden attractor corresponds to a qualitative change in behaviour from monostability to bi-stability. In the general case, a dynamical system may turn out to be multistable and have coexisting local attractors in the phase space. While trivial attractors, i.e. stable equilibrium points, can be easily found analytically or numerically, the search of periodic and chaotic attractors can turn out to be a challenging problem.

In fluid mechanics, the Rayleigh–Plesset equation or Besant–Rayleigh–Plesset equation is a nonlinear ordinary differential equation which governs the dynamics of a spherical bubble in an infinite body of incompressible fluid. Its general form is usually written as
Celso Grebogi is a Brazilian theoretical physicist who works in the area of chaos theory. He is one among the pioneers in the nonlinear and complex systems and chaos theory. Currently he works at the University of Aberdeen as the "Sixth Century Chair in Nonlinear and Complex Systems". He has done extensive research in the field of plasma physics before his work on the theory of dynamical systems. He and his colleagues have shown with a numerical example that one can convert a chaotic attractor to any one of numerous possible attracting time-periodic motions by making only small time-dependent perturbations of an available system parameter. This article is considered as one among the classic works in the control theory of chaos and their control method is known as the OGY method. He was listed in the 2016 Thomson Reuters Citation Laureates.

Edward Ott is an American physicist most noted for his contributions to the development of chaos theory.
Cavitation modelling is a type of computational fluid dynamic (CFD) that represents the flow of fluid during cavitation. It covers a wide range of applications, such as pumps, water turbines, pump inducers, and fuel cavitation in orifices as commonly encountered in fuel injection systems.
Michael Ghil is an American and European mathematician and physicist, focusing on the climate sciences and their interdisciplinary aspects. He is a founder of theoretical climate dynamics, as well as of advanced data assimilation methodology. He has systematically applied dynamical systems theory to planetary-scale flows, both atmospheric and oceanic. Ghil has used these methods to proceed from simple flows with high temporal regularity and spatial symmetry to the observed flows, with their complex behavior in space and time. His studies of climate variability on many time scales have used a full hierarchy of models, from the simplest ‘toy’ models all the way to atmospheric, oceanic and coupled general circulation models. Recently, Ghil has also worked on modeling and data analysis in population dynamics, macroeconomics, and the climate–economy–biosphere system.









