Charge-transfer insulators

Last updated July 18, 2024

Charge-transfer insulators are a class of materials predicted to be conductors following conventional band theory, but which are in fact insulators due to a charge-transfer process. Unlike in Mott insulators, where the insulating properties arise from electrons hopping between unit cells, the electrons in charge-transfer insulators move between atoms within the unit cell. In the Mott–Hubbard case, it's easier for electrons to transfer between two adjacent metal sites (on-site Coulomb interaction U); here we have an excitation corresponding to the Coulomb energy U with

$d^{n}d^{n}\rightarrow d^{n-1}d^{n+1},\quad \Delta E=U=U_{dd}$ .

In the charge-transfer case, the excitation happens from the anion (e.g., oxygen) p level to the metal d level with the charge-transfer energy Δ:

$d^{n}p^{6}\rightarrow d^{n+1}p^{5},\quad \Delta E=\Delta _{CT}$ .

U is determined by repulsive/exchange effects between the cation valence electrons. Δ is tuned by the chemistry between the cation and anion. One important difference is the creation of an oxygen p hole, corresponding to the change from a 'normal' ${\ce {O^2-}}$ to the ionic ${\ce {O-}}$ state.^[1] In this case the ligand hole is often denoted as ${\textstyle {\underline {L}}}$ .

Distinguishing between Mott-Hubbard and charge-transfer insulators can be done using the Zaanen-Sawatzky-Allen (ZSA) scheme.^[2]

Exchange interaction

Analogous to Mott insulators we also have to consider superexchange in charge-transfer insulators. One contribution is similar to the Mott case: the hopping of a d electron from one transition metal site to another and then back the same way. This process can be written as

$d_{i}^{n}p^{6}d_{j}^{n}\rightarrow d_{i}^{n}p^{5}d_{j}^{n+1}\rightarrow d_{i}^{n-1}p^{6}d_{j}^{n+1}\rightarrow d_{i}^{n}p^{5}d_{j}^{n+1}\rightarrow d_{i}^{n}p^{6}d_{j}^{n}$ .

This will result in an antiferromagnetic exchange (for nondegenerate d levels) with an exchange constant $J=J_{dd}$ .

$J_{dd}={\frac {2t_{dd}^{2}}{U_{dd}}}={\cfrac {2t_{pd}^{4}}{\Delta _{CT}^{2}U_{dd}}}$

In the charge-transfer insulator case

$d_{i}^{n}p^{6}d_{j}^{n}\rightarrow d_{i}^{n}p^{5}d_{j}^{n+1}\rightarrow d_{i}^{n+1}p^{4}d_{j}^{n+1}\rightarrow d_{i}^{n+1}p^{5}d_{j}^{n}\rightarrow d_{i}^{n}p^{6}d_{j}^{n}$ .

This process also yields an antiferromagnetic exchange $J_{pd}$ :

$J_{pd}={\cfrac {4t_{pd}^{4}}{\Delta _{CT}^{2}\cdot \left(2\Delta _{CT}+U_{pp}\right)}}$

The difference between these two possibilities is the intermediate state, which has one ligand hole for the first exchange ( $p^{6}\rightarrow p^{5}$ ) and two for the second ( $p^{6}\rightarrow p^{4}$ ).

The total exchange energy is the sum of both contributions:

$J_{total}={\cfrac {2t_{pd}^{4}}{\Delta _{CT}^{2}}}\cdot \left({\cfrac {1}{U_{dd}}}+{\cfrac {1}{\Delta _{CT}+{\tfrac {1}{2}}U_{pp}}}\right)$ .

Depending on the ratio of $U_{dd}{\text{ and }}\left(\Delta _{CT}+{\tfrac {1}{2}}U_{pp}\right)$ , the process is dominated by one of the terms and thus the resulting state is either Mott-Hubbard or charge-transfer insulating.^[1]

Related Research Articles

<span class="mw-page-title-main">Exciton</span> Quasiparticle which is a bound state of an electron and an electron hole

An electron and an electron hole that are attracted to each other by the Coulomb force can form a bound state called an exciton. It is an electrically neutral quasiparticle that exists mainly in condensed matter, including insulators, semiconductors, some metals, but also in certain atoms, molecules and liquids. The exciton is regarded as an elementary excitation that can transport energy without transporting net electric charge.

<span class="mw-page-title-main">Bremsstrahlung</span> Electromagnetic radiation due to deceleration of charged particles

In particle physics, bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

Capacitance is the capability of a material object or device to store electric charge. It is measured by the charge in response to a difference in electric potential, expressed as the ratio of those quantities. Commonly recognized are two closely related notions of capacitance: self capacitance and mutual capacitance. An object that can be electrically charged exhibits self capacitance, for which the electric potential is measured between the object and ground. Mutual capacitance is measured between two components, and is particularly important in the operation of the capacitor, an elementary linear electronic component designed to add capacitance to an electric circuit.

Density functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry.

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as $Where:$

In the calculus of variations and classical mechanics, the Euler–Lagrange equations are a system of second-order ordinary differential equations whose solutions are stationary points of the given action functional. The equations were discovered in the 1750s by Swiss mathematician Leonhard Euler and Italian mathematician Joseph-Louis Lagrange.

A p–n junction is a combination of two types of semiconductor materials, p-type and n-type, in a single crystal. The "n" (negative) side contains freely-moving electrons, while the "p" (positive) side contains freely-moving electron holes. Connecting the two materials causes creation of a depletion region near the boundary, as the free electrons fill the available holes, which in turn allows electric current to pass through the junction only in one direction.

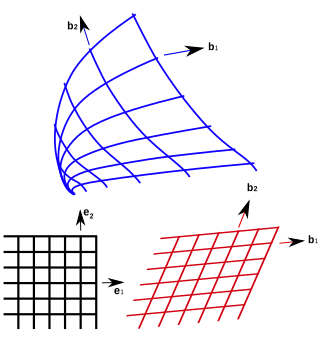
<span class="mw-page-title-main">Curvilinear coordinates</span> Coordinate system whose directions vary in space

In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name curvilinear coordinates, coined by the French mathematician Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved.

The rectangular function is defined as

In magnetism, the Curie–Weiss law describes the magnetic susceptibility $χ$ of a ferromagnet in the paramagnetic region above the Curie temperature:

<span class="mw-page-title-main">Hubbard model</span> Approximate model used to describe the transition between conducting and insulating systems

The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard.

In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically deforming materials and other fluids and biological soft tissue.

<span class="mw-page-title-main">Mott insulator</span> Materials classically predicted to be conductors, that are actually insulators

Mott insulators are a class of materials that are expected to conduct electricity according to conventional band theories, but turn out to be insulators. These insulators fail to be correctly described by band theories of solids due to their strong electron–electron interactions, which are not considered in conventional band theory. A Mott transition is a transition from a metal to an insulator, driven by the strong interactions between electrons. One of the simplest models that can capture Mott transition is the Hubbard model.

In solid-state physics, the tight-binding model is an approach to the calculation of electronic band structure using an approximate set of wave functions based upon superposition of wave functions for isolated atoms located at each atomic site. The method is closely related to the LCAO method used in chemistry. Tight-binding models are applied to a wide variety of solids. The model gives good qualitative results in many cases and can be combined with other models that give better results where the tight-binding model fails. Though the tight-binding model is a one-electron model, the model also provides a basis for more advanced calculations like the calculation of surface states and application to various kinds of many-body problem and quasiparticle calculations.

In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density is the quantity of charge per unit volume, measured in the SI system in coulombs per cubic meter (C⋅m⁻³), at any point in a volume. Surface charge density (σ) is the quantity of charge per unit area, measured in coulombs per square meter (C⋅m⁻²), at any point on a surface charge distribution on a two dimensional surface. Linear charge density (λ) is the quantity of charge per unit length, measured in coulombs per meter (C⋅m⁻¹), at any point on a line charge distribution. Charge density can be either positive or negative, since electric charge can be either positive or negative.

In theoretical chemistry, Marcus theory is a theory originally developed by Rudolph A. Marcus, starting in 1956, to explain the rates of electron transfer reactions – the rate at which an electron can move or jump from one chemical species (called the electron donor) to another (called the electron acceptor). It was originally formulated to address outer sphere electron transfer reactions, in which the two chemical species only change in their charge with an electron jumping (e.g. the oxidation of an ion like Fe²⁺/Fe³⁺), but do not undergo large structural changes. It was extended to include inner sphere electron transfer contributions, in which a change of distances or geometry in the solvation or coordination shells of the two chemical species is taken into account (the Fe-O distances in Fe(H₂O)²⁺ and Fe(H₂O)³⁺ are different).

The Bose–Hubbard model gives a description of the physics of interacting spinless bosons on a lattice. It is closely related to the Hubbard model that originated in solid-state physics as an approximate description of superconducting systems and the motion of electrons between the atoms of a crystalline solid. The model was introduced by Gersch and Knollman in 1963 in the context of granular superconductors. The model rose to prominence in the 1980s after it was found to capture the essence of the superfluid-insulator transition in a way that was much more mathematically tractable than fermionic metal-insulator models.

Charge ordering (CO) is a phase transition occurring mostly in strongly correlated materials such as transition metal oxides or organic conductors. Due to the strong interaction between electrons, charges are localized on different sites leading to a disproportionation and an ordered superlattice. It appears in different patterns ranging from vertical to horizontal stripes to a checkerboard–like pattern , and it is not limited to the two-dimensional case. The charge order transition is accompanied by symmetry breaking and may lead to ferroelectricity. It is often found in close proximity to superconductivity and colossal magnetoresistance.

The Thomas–Fermi (TF) model, named after Llewellyn Thomas and Enrico Fermi, is a quantum mechanical theory for the electronic structure of many-body systems developed semiclassically shortly after the introduction of the Schrödinger equation. It stands separate from wave function theory as being formulated in terms of the electronic density alone and as such is viewed as a precursor to modern density functional theory. The Thomas–Fermi model is correct only in the limit of an infinite nuclear charge. Using the approximation for realistic systems yields poor quantitative predictions, even failing to reproduce some general features of the density such as shell structure in atoms and Friedel oscillations in solids. It has, however, found modern applications in many fields through the ability to extract qualitative trends analytically and with the ease at which the model can be solved. The kinetic energy expression of Thomas–Fermi theory is also used as a component in more sophisticated density approximation to the kinetic energy within modern orbital-free density functional theory.

In quantum computing, and more specifically in superconducting quantum computing, the phase qubit is a superconducting device based on the superconductor–insulator–superconductor (SIS) Josephson junction, designed to operate as a quantum bit, or qubit.

References

1 2 Khomskii, Daniel I. (2014). Transition Metal Compounds. Cambridge: Cambridge University Press. doi:10.1017/cbo9781139096782. ISBN 978-1-107-02017-7.
↑ Zaanen, J.; Sawatzky, G. A.; Allen, J. W. (1985-07-22). "Band gaps and electronic structure of transition-metal compounds". Physical Review Letters. 55 (4): 418–421. Bibcode:1985PhRvL..55..418Z. doi:10.1103/PhysRevLett.55.418. hdl: 1887/5216 . PMID 10032345.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 Khomskii, Daniel I. (2014). Transition Metal Compounds. Cambridge: Cambridge University Press. doi:10.1017/cbo9781139096782. ISBN 978-1-107-02017-7.

[2] Zaanen, J.; Sawatzky, G. A.; Allen, J. W. (1985-07-22). "Band gaps and electronic structure of transition-metal compounds". Physical Review Letters. 55 (4): 418–421. Bibcode:1985PhRvL..55..418Z. doi:10.1103/PhysRevLett.55.418. hdl: 1887/5216 . PMID 10032345.

[1]

[2]