Related Research Articles
Automated theorem proving is a subfield of automated reasoning and mathematical logic dealing with proving mathematical theorems by computer programs. Automated reasoning over mathematical proof was a major motivating factor for the development of computer science.
In logic and computer science, specifically automated reasoning, unification is an algorithmic process of solving equations between symbolic expressions, each of the form Left-hand side = Right-hand side. For example, using x,y,z as variables, and taking f to be an uninterpreted function, the singleton equation set { f(1,y) = f(x,2) } is a syntactic first-order unification problem that has the substitution { x ↦ 1, y ↦ 2 } as its only solution.
E is a high-performance theorem prover for full first-order logic with equality. It is based on the equational superposition calculus and uses a purely equational paradigm. It has been integrated into other theorem provers and it has been among the best-placed systems in several theorem proving competitions. E is developed by Stephan Schulz, originally in the Automated Reasoning Group at TU Munich, now at Baden-Württemberg Cooperative State University Stuttgart.

In computer science and mathematical logic, a proof assistant or interactive theorem prover is a software tool to assist with the development of formal proofs by human–machine collaboration. This involves some sort of interactive proof editor, or other interface, with which a human can guide the search for proofs, the details of which are stored in, and some steps provided by, a computer.
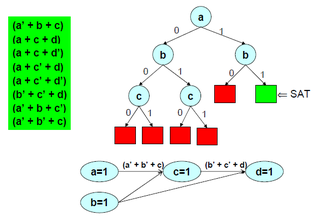
In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem.
In computer science, in particular in knowledge representation and reasoning and metalogic, the area of automated reasoning is dedicated to understanding different aspects of reasoning. The study of automated reasoning helps produce computer programs that allow computers to reason completely, or nearly completely, automatically. Although automated reasoning is considered a sub-field of artificial intelligence, it also has connections with theoretical computer science and philosophy.
In computer science and mathematical logic, satisfiability modulo theories (SMT) is the problem of determining whether a mathematical formula is satisfiable. It generalizes the Boolean satisfiability problem (SAT) to more complex formulas involving real numbers, integers, and/or various data structures such as lists, arrays, bit vectors, and strings. The name is derived from the fact that these expressions are interpreted within ("modulo") a certain formal theory in first-order logic with equality. SMT solvers are tools that aim to solve the SMT problem for a practical subset of inputs. SMT solvers such as Z3 and cvc5 have been used as a building block for a wide range of applications across computer science, including in automated theorem proving, program analysis, program verification, and software testing.

Alan Richard Bundy is a professor at the School of Informatics at the University of Edinburgh, known for his contributions to automated reasoning, especially to proof planning, the use of meta-level reasoning to guide proof search.
Keith Leonard Clark is an Emeritus Professor in the Department of Computing at Imperial College London, England.
In computer science, termination analysis is program analysis which attempts to determine whether the evaluation of a given program halts for each input. This means to determine whether the input program computes a total function.
Many-sorted logic can reflect formally our intention not to handle the universe as a homogeneous collection of objects, but to partition it in a way that is similar to types in typeful programming. Both functional and assertive "parts of speech" in the language of the logic reflect this typeful partitioning of the universe, even on the syntax level: substitution and argument passing can be done only accordingly, respecting the "sorts".
Computational logic is the use of logic to perform or reason about computation. It bears a similar relationship to computer science and engineering as mathematical logic bears to mathematics and as philosophical logic bears to philosophy. It is an alternative term for "logic in computer science".
SNARK, , is a theorem prover for multi-sorted first-order logic intended for applications in artificial intelligence and software engineering, developed at SRI International.
Donald W. Loveland is a professor emeritus of computer science at Duke University who specializes in artificial intelligence. He is well known for the Davis–Putnam–Logemann–Loveland algorithm.
In computer programming, Walther recursion is a method of analysing recursive functions that can determine if the function is definitely terminating, given finite inputs. It allows a more natural style of expressing computation than simply using primitive recursive functions.
A verification condition generator is a common sub-component of an automated program verifier that synthesizes formal verification conditions by analyzing a program's source code using a method based upon Hoare logic. VC generators may require that the source code contains logical annotations provided by the programmer or the compiler such as pre/post-conditions and loop invariants. VC generators are often coupled with SMT solvers in the backend of a program verifier. After a verification condition generator has created the verification conditions they are passed to an automated theorem prover, which can then formally prove the correctness of the code.
Anti-unification is the process of constructing a generalization common to two given symbolic expressions. As in unification, several frameworks are distinguished depending on which expressions are allowed, and which expressions are considered equal. If variables representing functions are allowed in an expression, the process is called "higher-order anti-unification", otherwise "first-order anti-unification". If the generalization is required to have an instance literally equal to each input expression, the process is called "syntactical anti-unification", otherwise "E-anti-unification", or "anti-unification modulo theory".
Nachum Dershowitz is an Israeli computer scientist, known e.g. for the Dershowitz–Manna ordering and the multiset path ordering used to prove termination of term rewrite systems.
Tobias Nipkow is a German computer scientist.
TPTP is a freely available collection of problems for automated theorem proving. It is used to evaluate the efficacy of automated reasoning algorithms. Problems are expressed in a simple text-based format for first order logic or higher-order logic. TPTP is used as the source of some problems in CASC.
References
- ↑ Simon Siegler and Nathan Wasser, ed. (2010). "Preface". Verification, Induction, Termination Analysis —- Festschrift for Christoph Walther on the Occasion of His 60th Birthday. LNAI. Vol. 6463. Springer. ISBN 978-3-642-17171-0.
- ↑ Professuren und Gruppenleitungen Archived 2015-02-21 at the Wayback Machine (Section Emeriti und Professoren im Ruhestand) at Darmstadt University Web Site