
In geometry, Clifford's theorems, named after the English geometer William Kingdon Clifford, are a sequence of theorems relating to intersections of circles.

In geometry, Clifford's theorems, named after the English geometer William Kingdon Clifford, are a sequence of theorems relating to intersections of circles.
The first theorem considers any four circles passing through a common point M and otherwise in general position, meaning that there are six additional points where exactly two of the circles cross and that no three of these crossing points are collinear. Every set of three of these four circles has among them three crossing points, and (by the assumption of non-collinearity) there exists a circle passing through these three crossing points. The conclusion is that, like the first set of four circles, the second set of four circles defined in this way all pass through a single point P (in general not the same point as M).
The second theorem considers five circles in general position passing through a single point M. Each subset of four circles defines a new point P according to the first theorem. Then these five points all lie on a single circle C.
The third theorem considers six circles in general position that pass through a single point M. Each subset of five circles defines a new circle by the second theorem. Then these six new circles C all pass through a single point.
The sequence of theorems can be continued indefinitely.

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.

In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice-versa.

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible, which is referred to as special position. Its precise meaning differs in different settings.
In geometry, a degenerate conic is a conic that fails to be an irreducible curve. This means that the defining equation is factorable over the complex numbers as the product of two linear polynomials.

In geometry, a set of points are said to be concyclic if they lie on a common circle. All concyclic points are at the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.

In the branch of mathematics known as Euclidean geometry, the Poncelet–Steiner theorem is one of several results concerning compass and straightedge constructions with additional restrictions imposed. This result states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone, provided that a single circle and its centre are given. This theorem is related to the rusty compass equivalence.

In projective geometry, Pascal's theorem states that if six arbitrary points are chosen on a conic and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon meet at three points which lie on a straight line, called the Pascal line of the hexagon. It is named after Blaise Pascal.

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.
In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An incidence structure is what is obtained when all other concepts are removed and all that remains is the data about which points lie on which lines. Even with this severe limitation, theorems can be proved and interesting facts emerge concerning this structure. Such fundamental results remain valid when additional concepts are added to form a richer geometry. It sometimes happens that authors blur the distinction between a study and the objects of that study, so it is not surprising to find that some authors refer to incidence structures as incidence geometries.

In mathematics, the "happy ending problem" is the following statement:

In mathematics, specifically in incidence geometry and especially in projective geometry, a complete quadrangle is a system of geometric objects consisting of any four points in a plane, no three of which are on a common line, and of the six lines connecting the six pairs of points. Dually, a complete quadrilateral is a system of four lines, no three of which pass through the same point, and the six points of intersection of these lines. The complete quadrangle was called a tetrastigm by Lachlan (1893), and the complete quadrilateral was called a tetragram; those terms are occasionally still used.

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.
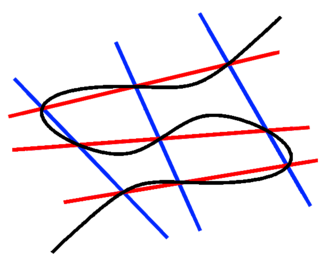
In mathematics, the Cayley–Bacharach theorem is a statement about cubic curves in the projective plane P2. The original form states:
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

In geometry, Monge's theorem, named after Gaspard Monge, states that for any three circles in a plane, none of which is completely inside one of the others, the intersection points of each of the three pairs of external tangent lines are collinear.

In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles, where n is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usual closed Steiner chains, the first and last (nth) circles are also tangent to each other; by contrast, in open Steiner chains, they need not be. The given circles α and β do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse or a hyperbola, respectively.

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.

Miquel's theorem is a result in geometry, named after Auguste Miquel, concerning the intersection of three circles, each drawn through one vertex of a triangle and two points on its adjacent sides. It is one of several results concerning circles in Euclidean geometry due to Miquel, whose work was published in Liouville's newly founded journal Journal de mathématiques pures et appliquées.
In Euclidean and projective geometry, just as two (distinct) points determine a line, five points determine a conic. There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.