In geometry, the five circles theorem states that, given five circles centered on a common sixth circle and intersecting each other chainwise on the same circle, the lines joining their second intersection points forms a pentagram whose points lie on the circles themselves.
In geometry, an orthocentric system is a set of four points on a plane, one of which is the orthocenter of the triangle formed by the other three.
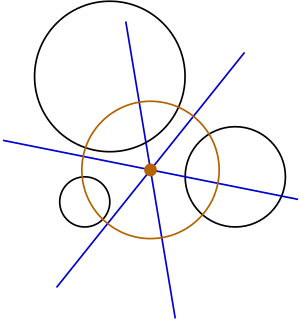
In geometry, the power center of three circles, also called the radical center, is the intersection point of the three radical axes of the pairs of circles. If the radical center lies outside of all three circles, then it is the center of the unique circle that intersects the three given circles orthogonally; the construction of this orthogonal circle corresponds to Monge's problem. This is a special case of the three conics theorem.
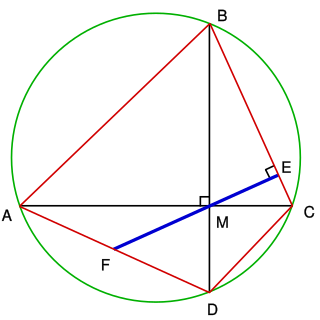
In geometry, Brahmagupta's theorem states that if a cyclic quadrilateral is orthodiagonal, then the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side. It is named after the Indian mathematician Brahmagupta (598-668).
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter–Dynkin diagram of
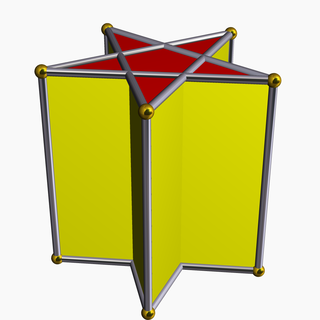
In geometry, the pentagrammic prism is one of an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.
In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.
In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.
In geometry, the great icosahedron is one of four Kepler-Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of
In geometry, the truncated great dodecahedron is a nonconvex uniform polyhedron, indexed as U37. It has 24 faces (12 pentagrams and 12 decagons), 90 edges, and 60 vertices. It is given a Schläfli symbol t{5,5⁄2}.
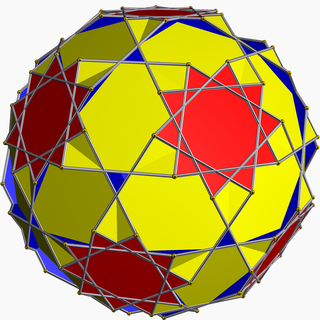
In geometry, the truncated dodecadodecahedron (or stellatruncated dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U59. It is given a Schläfli symbol t0,1,2{5⁄3,5}. It has 54 faces (30 squares, 12 decagons, and 12 decagrams), 180 edges, and 120 vertices. The central region of the polyhedron is connected to the exterior via 20 small triangular holes.
In geometry, Jung's theorem is an inequality between the diameter of a set of points in any Euclidean space and the radius of the minimum enclosing ball of that set. It is named after Heinrich Jung, who first studied this inequality in 1901. Algorithms also exist to solve the smallest-circle problem explicitly.
In geometry, a set of Johnson circles comprises three circles of equal radius r sharing one common point of intersection H. In such a configuration the circles usually have a total of four intersections : the common point H that they all share, and for each of the three pairs of circles one more intersection point. If any two of the circles happen to osculate, they only have H as a common point, and it will then be considered that H be their 2-wise intersection as well; if they should coincide we declare their 2-wise intersection be the point diametrically opposite H. The three 2-wise intersection points define the reference triangle of the figure. The concept is named after Roger Arthur Johnson.
In Euclidean plane geometry, Lester's theorem states that in any scalene triangle, the two Fermat points, the nine-point center, and the circumcenter lie on the same circle. The result is named after June Lester, who published it in 1997, and the circle through these points was called the Lester circle by Clark Kimberling. Lester proved the result by using the properties of complex numbers; subsequent authors have given elementary proofs, proofs using vector arithmetic, and computerized proofs.
In geometry, the six circles theorem relates to a chain of six circles together with a triangle, such that each circle is tangent to two sides of the triangle and also to the preceding circle in the chain. The chain closes, in the sense that the sixth circle is always tangent to the first circle. It is assumed in this construction that all circles lie within the triangle, and all points of tangency lie on the sides of the triangle. If the problem is generalized to allow circles that may not be within the triangle, and points of tangency on the lines extending the sides of the triangle, then the sequence of circles eventually reaches a periodic sequence of six circles, but may take arbitrarily many steps to reach this periodicity.
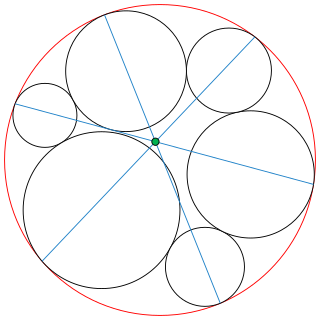
In geometry, the seven circles theorem is a theorem about a certain arrangement of seven circles in the Euclidean plane. Specifically, given a chain of six circles all tangent to a seventh circle and each tangent to its two neighbors, the three lines drawn between opposite pairs of the points of tangency on the seventh circle all pass through the same point. Though elementary in nature, this theorem was not discovered until 1974.
Miquel's theorem is a result in geometry, named after Auguste Miquel, concerning the intersection of three circles, each drawn through one vertex of a triangle and two points on its adjacent sides. It is one of several results concerning circles in Euclidean geometry due to Miquel, whose work was published in Liouville's newly founded journal Journal de mathématiques pures et appliquées.
In geometry, Clifford's theorems, named after the English geometer William Kingdon Clifford, are a sequence of theorems relating to intersections of circles.
In geometry, tangent circles are circles in a common plane that intersect in a single point. There are two types of tangency: internal and external. Many problems and constructions in geometry are related to tangent circles; such problems often have real-life applications such as trilateration and maximizing the use of materials.
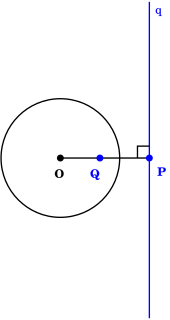
In geometry, the pole and polar are respectively a point and a line that have a unique reciprocal relationship with respect to a given conic section.
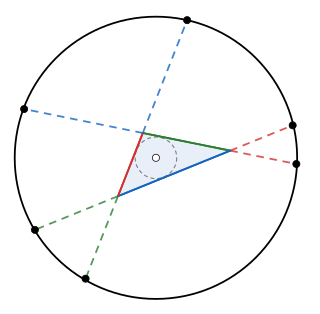
In plane geometry, the Conway circle theorem states that when the sides meeting at each vertex of a triangle are extended by the length of the opposite side, the six endpoints of the three resulting line segments lie on a circle whose centre is the incentre of the triangle. The circle on which these six points lie is called the Conway circle of the triangle. The theorem and circle are named after mathematician John Horton Conway.