
OpenGL is a cross-language, cross-platform application programming interface (API) for rendering 2D and 3D vector graphics. The API is typically used to interact with a graphics processing unit (GPU), to achieve hardware-accelerated rendering.

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example,
In linear algebra, the trace of a square matrix A, denoted tr(A), is defined to be the sum of elements on the main diagonal of A. The trace is only defined for a square matrix.

In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcul, are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix.
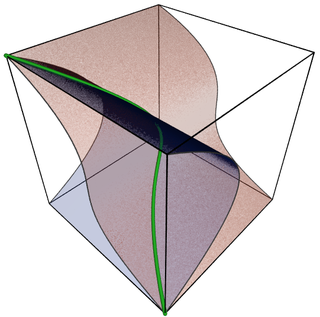
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.

A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.
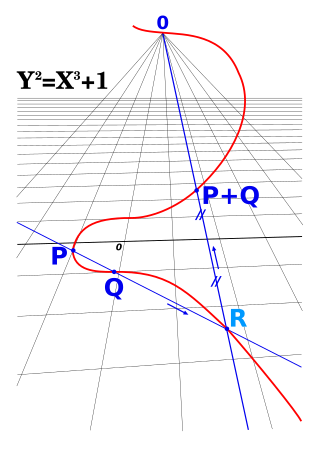
In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .

In analytic geometry, spatial transformations in the 3-dimensional Euclidean space are distinguished into active or alibi transformations, and passive or alias transformations. An active transformation is a transformation which actually changes the physical position of a point, or rigid body, which can be defined in the absence of a coordinate system; whereas a passive transformation is merely a change in the coordinate system in which the object is described. By transformation, mathematicians usually refer to active transformations, while physicists and engineers could mean either. Both types of transformation can be represented by a combination of a translation and a linear transformation.
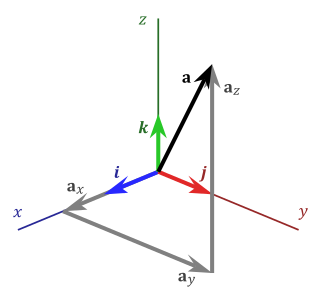
In mathematics, the standard basis (also called natural basis or canonical basis) of a coordinate vector space (such as or ) is the set of vectors whose components are all zero, except one that equals 1. For example, in the case of the Euclidean plane formed by the pairs (x, y) of real numbers, the standard basis is formed by the vectors

In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex. The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex.

OpenGL for Embedded Systems is a subset of the OpenGL computer graphics rendering application programming interface (API) for rendering 2D and 3D computer graphics such as those used by video games, typically hardware-accelerated using a graphics processing unit (GPU). It is designed for embedded systems like smartphones, tablet computers, video game consoles and PDAs. OpenGL ES is the "most widely deployed 3D graphics API in history".
In computer graphics, a computer graphics pipeline, rendering pipeline or simply graphics pipeline, is a conceptual model that describes what steps a graphics system needs to perform to render a 3D scene to a 2D screen. Once a 3D model has been created, for instance in a video game or any other 3D computer animation, the graphics pipeline is the process of turning that 3D model into what the computer displays. Because the steps required for this operation depend on the software and hardware used and the desired display characteristics, there is no universal graphics pipeline suitable for all cases. However, graphics application programming interfaces (APIs) such as Direct3D and OpenGL were created to unify similar steps and to control the graphics pipeline of a given hardware accelerator. These APIs abstract the underlying hardware and keep the programmer away from writing code to manipulate the graphics hardware accelerators.
Clipping, in the context of computer graphics, is a method to selectively enable or disable rendering operations within a defined region of interest. Mathematically, clipping can be described using the terminology of constructive geometry. A rendering algorithm only draws pixels in the intersection between the clip region and the scene model. Lines and surfaces outside the view volume are removed.
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation.

In geometry, a three-dimensional space is a mathematical structure in which three values (coordinates) are required to determine the position of a point. More specifically, the three-dimensional space is the Euclidean space of dimension three that models physical space.
In computer vision, the essential matrix is a matrix, that relates corresponding points in stereo images assuming that the cameras satisfy the pinhole camera model.
In computer vision a camera matrix or (camera) projection matrix is a matrix which describes the mapping of a pinhole camera from 3D points in the world to 2D points in an image.
In algebra, a multilinear polynomial is a multivariate polynomial that is linear in each of its variables separately, but not necessarily simultaneously. It is a polynomial in which no variable occurs to a power of 2 or higher; that is, each monomial is a constant times a product of distinct variables. For example f(x,y,z) = 3xy + 2.5 y - 7z is a multilinear polynomial of degree 2 whereas f(x,y,z) = x² +4y is not. The degree of a multilinear polynomial is the maximum number of distinct variables occurring in any monomial.
In mathematics, the closed-subgroup theorem is a theorem in the theory of Lie groups. It states that if H is a closed subgroup of a Lie group G, then H is an embedded Lie group with the smooth structure agreeing with the embedding. One of several results known as Cartan's theorem, it was first published in 1930 by Élie Cartan, who was inspired by John von Neumann's 1929 proof of a special case for groups of linear transformations.
This is a glossary of terms relating to computer graphics.



















