
Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

Romanesque architecture is an architectural style of medieval Europe that was predominant in the 11th and 12th centuries. The style eventually developed into the Gothic style with the shape of the arches providing a simple distinction: the Romanesque is characterized by semicircular arches, while the Gothic is marked by the pointed arches. The Romanesque emerged nearly simultaneously in multiple countries ; its examples can be found across the continent, making it the first pan-European architectural style since Imperial Roman architecture. Similarly to Gothic, the name of the style was transferred onto the contemporary Romanesque art.

A dome is an architectural element similar to the hollow upper half of a sphere. There is significant overlap with the term cupola, which may also refer to a dome or a structure on top of a dome. The precise definition of a dome has been a matter of controversy and there are a wide variety of forms and specialized terms to describe them.
The Method of Mechanical Theorems, also referred to as The Method, is one of the major surviving works of the ancient Greek polymath Archimedes. The Method takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles. The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the center of weights of figures (centroid) and the law of the lever, which were demonstrated by Archimedes in On the Equilibrium of Planes.

A rib vault or ribbed vault is an architectural feature for covering a wide space, such as a church nave, composed of a framework of crossed or diagonal arched ribs. Variations were used in Roman architecture, Byzantine architecture, Islamic architecture, Romanesque architecture, and especially Gothic architecture. Thin stone panels fill the space between the ribs. This greatly reduced the weight and thus the outward thrust of the vault. The ribs transmit the load downward and outward to specific points, usually rows of columns or piers. This feature allowed architects of Gothic cathedrals to make higher and thinner walls and much larger windows.

A barrel vault, also known as a tunnel vault, wagon vault or wagonhead vault, is an architectural element formed by the extrusion of a single curve along a given distance. The curves are typically circular in shape, lending a semi-cylindrical appearance to the total design. The barrel vault is the simplest form of a vault: effectively a series of arches placed side by side. It is a form of barrel roof.

A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.

In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation.
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the nth polygon and the containing shape will become arbitrarily small as n becomes large. As this difference becomes arbitrarily small, the possible values for the area of the shape are systematically "exhausted" by the lower bound areas successively established by the sequence members.

A groin vault or groined vault is produced by the intersection at right angles of two barrel vaults. The word "groin" refers to the edge between the intersecting vaults. Sometimes the arches of groin vaults are pointed instead of round. In comparison with a barrel vault, a groin vault provides good economies of material and labor. The thrust is concentrated along the groins or arrises, so the vault need only be abutted at its four corners.
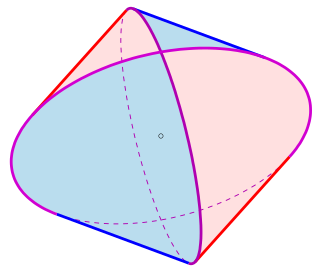
In geometry, a Steinmetz solid is the solid body obtained as the intersection of two or three cylinders of equal radius at right angles. Each of the curves of the intersection of two cylinders is an ellipse.

In architecture, a vault is a self-supporting arched form, usually of stone or brick, serving to cover a space with a ceiling or roof. As in building an arch, a temporary support is needed while rings of voussoirs are constructed and the rings placed in position. Until the topmost voussoir, the keystone, is positioned, the vault is not self-supporting. Where timber is easily obtained, this temporary support is provided by centering consisting of a framed truss with a semicircular or segmental head, which supports the voussoirs until the ring of the whole arch is completed.

In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:

Domes were a characteristic element of the architecture of Ancient Rome and of its medieval continuation, the Byzantine Empire. They had widespread influence on contemporary and later styles, from Russian and Ottoman architecture to the Italian Renaissance and modern revivals. The domes were customarily hemispherical, although octagonal and segmented shapes are also known, and they developed in form, use, and structure over the centuries. Early examples rested directly on the rotunda walls of round rooms and featured a central oculus for ventilation and light. Pendentives became common in the Byzantine period, provided support for domes over square spaces.

The early domes of the Middle Ages, particularly in those areas recently under Byzantine control, were an extension of earlier Roman architecture. The domed church architecture of Italy from the sixth to the eighth centuries followed that of the Byzantine provinces and, although this influence diminishes under Charlemagne, it continued on in Venice, Southern Italy, and Sicily. Charlemagne's Palatine Chapel is a notable exception, being influenced by Byzantine models from Ravenna and Constantinople. The Dome of the Rock, an Umayyad Muslim religious shrine built in Jerusalem, was designed similarly to nearby Byzantine martyria and Christian churches. Domes were also built as part of Muslim palaces, throne halls, pavilions, and baths, and blended elements of both Byzantine and Persian architecture, using both pendentives and squinches. The origin of the crossed-arch dome type is debated, but the earliest known example is from the tenth century at the Great Mosque of Córdoba. In Egypt, a "keel" shaped dome profile was characteristic of Fatimid architecture. The use of squinches became widespread in the Islamic world by the tenth and eleventh centuries. Bulbous domes were used to cover large buildings in Syria after the eleventh century, following an architectural revival there, and the present shape of the Dome of the Rock's dome likely dates from this time.

De quinque corporibus regularibus is a book on the geometry of polyhedra written in the 1480s or early 1490s by Italian painter and mathematician Piero della Francesca. It is a manuscript, in the Latin language; its title means [the little book] on the five regular solids. It is one of three books known to have been written by della Francesca.

Curved structures are constructions generated by one or more generatrices through geometrical operations. They traditionally differentiate from the other most diffused construction technology, namely the post and lintel, which results from the addition of regular and linear architectural elements.


















