In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

In computer science, a search algorithm is an algorithm designed to solve a search problem. Search algorithms work to retrieve information stored within particular data structure, or calculated in the search space of a problem domain, with either discrete or continuous values.

Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. Extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored.
In computer science, brute-force search or exhaustive search, also known as generate and test, is a very general problem-solving technique and algorithmic paradigm that consists of systematically checking all possible candidates for whether or not each candidate satisfies the problem's statement.
Alpha–beta pruning is a search algorithm that seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree. It is an adversarial search algorithm used commonly for machine playing of two-player combinatorial games. It stops evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.

Computer Go is the field of artificial intelligence (AI) dedicated to creating a computer program that plays the traditional board game Go. The field is sharply divided into two eras. Before 2015, the programs of the era were weak. The best efforts of the 1980s and 1990s produced only AIs that could be defeated by beginners, and AIs of the early 2000s were intermediate level at best. Professionals could defeat these programs even given handicaps of 10+ stones in favor of the AI. Many of the algorithms such as alpha-beta minimax that performed well as AIs for checkers and chess fell apart on Go's 19x19 board, as there were too many branching possibilities to consider. Creation of a human professional quality program with the techniques and hardware of the time was out of reach. Some AI researchers speculated that the problem was unsolvable without creation of human-like AI.
In the context of combinatorial game theory, which typically studies sequential games with perfect information, a game tree is a graph representing all possible game states within such a game. Such games include well-known ones such as chess, checkers, Go, and tic-tac-toe. This can be used to measure the complexity of a game, as it represents all the possible ways a game can pan out. Due to the large game trees of complex games such as chess, algorithms that are designed to play this class of games will use partial game trees, which makes computation feasible on modern computers. Various methods exist to solve game trees. If a complete game tree can be generated, a deterministic algorithm, such as backward induction or retrograde analysis can be used. Randomized algorithms and minmax algorithms such as MCTS can be used in cases where a complete game tree is not feasible.

Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position that the players take turns changing in defined ways or moves to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field.
Combinatorial game theory measures game complexity in several ways:
- State-space complexity,
- Game tree size,
- Decision complexity,
- Game-tree complexity,
- Computational complexity.
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures.

Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.
Branch and bound is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution. It is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm.
State space search is a process used in the field of computer science, including artificial intelligence (AI), in which successive configurations or states of an instance are considered, with the intention of finding a goal state with the desired property.

In computer science, a state space is a discrete space representing the set of all possible configurations of a "system". It is a useful abstraction for reasoning about the behavior of a given system and is widely used in the fields of artificial intelligence and game theory.
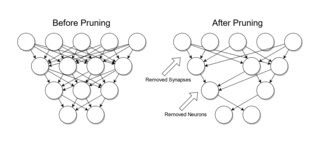
Pruning is a data compression technique in machine learning and search algorithms that reduces the size of decision trees by removing sections of the tree that are non-critical and redundant to classify instances. Pruning reduces the complexity of the final classifier, and hence improves predictive accuracy by the reduction of overfitting.
In mathematical optimization and computer science, heuristic is a technique designed for problem solving more quickly when classic methods are too slow for finding an exact or approximate solution, or when classic methods fail to find any exact solution in a search space. This is achieved by trading optimality, completeness, accuracy, or precision for speed. In a way, it can be considered a shortcut.
Quantum complexity theory is the subfield of computational complexity theory that deals with complexity classes defined using quantum computers, a computational model based on quantum mechanics. It studies the hardness of computational problems in relation to these complexity classes, as well as the relationship between quantum complexity classes and classical complexity classes.
Distributed tree search (DTS) algorithm is a class of algorithms for searching values in an efficient and distributed manner. Their purpose is to iterate through a tree by working along multiple branches in parallel and merging the results of each branch into one common solution, in order to minimize time spent searching for a value in a tree-like data structure.
In computer science, an enumeration algorithm is an algorithm that enumerates the answers to a computational problem. Formally, such an algorithm applies to problems that take an input and produce a list of solutions, similarly to function problems. For each input, the enumeration algorithm must produce the list of all solutions, without duplicates, and then halt. The performance of an enumeration algorithm is measured in terms of the time required to produce the solutions, either in terms of the total time required to produce all solutions, or in terms of the maximal delay between two consecutive solutions and in terms of a preprocessing time, counted as the time before outputting the first solution. This complexity can be expressed in terms of the size of the input, the size of each individual output, or the total size of the set of all outputs, similarly to what is done with output-sensitive algorithms.






