Related Research Articles
A discrete element method (DEM), also called a distinct element method, is any of a family of numerical methods for computing the motion and effect of a large number of small particles. Though DEM is very closely related to molecular dynamics, the method is generally distinguished by its inclusion of rotational degrees-of-freedom as well as stateful contact and often complicated geometries. With advances in computing power and numerical algorithms for nearest neighbor sorting, it has become possible to numerically simulate millions of particles on a single processor. Today DEM is becoming widely accepted as an effective method of addressing engineering problems in granular and discontinuous materials, especially in granular flows, powder mechanics, and rock mechanics. DEM has been extended into the Extended Discrete Element Method taking heat transfer, chemical reaction and coupling to CFD and FEM into account.

A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact. The constituents that compose granular material are large enough such that they are not subject to thermal motion fluctuations. Thus, the lower size limit for grains in granular material is about 1 μm. On the upper size limit, the physics of granular materials may be applied to ice floes where the individual grains are icebergs and to asteroid belts of the Solar System with individual grains being asteroids.

Soil mechanics is a branch of soil physics and applied mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids and other matter. Along with rock mechanics, soil mechanics provides the theoretical basis for analysis in geotechnical engineering, a subdiscipline of civil engineering, and engineering geology, a subdiscipline of geology. Soil mechanics is used to analyze the deformations of and flow of fluids within natural and man-made structures that are supported on or made of soil, or structures that are buried in soils. Example applications are building and bridge foundations, retaining walls, dams, and buried pipeline systems. Principles of soil mechanics are also used in related disciplines such as geophysical engineering, coastal engineering, agricultural engineering, hydrology and soil physics.
Discontinuous deformation analysis (DDA) is a type of discrete element method (DEM) originally proposed by Shi in 1988. DDA is somewhat similar to the finite element method for solving stress-displacement problems, but accounts for the interaction of independent particles (blocks) along discontinuities in fractured and jointed rock masses. DDA is typically formulated as a work-energy method, and can be derived using the principle of minimum potential energy or by using Hamilton's principle. Once the equations of motion are discretized, a step-wise linear time marching scheme in the Newmark family is used for the solution of the equations of motion. The relation between adjacent blocks is governed by equations of contact interpenetration and accounts for friction. DDA adopts a stepwise approach to solve for the large displacements that accompany discontinuous movements between blocks. The blocks are said to be "simply deformable". Since the method accounts for the inertial forces of the blocks' mass, it can be used to solve the full dynamic problem of block motion.

A shear band is a narrow zone of intense shearing strain, usually of plastic nature, developing during severe deformation of ductile materials. As an example, a soil specimen is shown in Fig. 1, after an axialsymmetric compression test. Initially the sample was cylindrical in shape and, since symmetry was tried to be preserved during the test, the cylindrical shape was maintained for a while during the test and the deformation was homogeneous, but at extreme loading two X-shaped shear bands had formed and the subsequent deformation was strongly localized.

Shear strength is a term used in soil mechanics to describe the magnitude of the shear stress that a soil can sustain. The shear resistance of soil is a result of friction and interlocking of particles, and possibly cementation or bonding at particle contacts. Due to interlocking, particulate material may expand or contract in volume as it is subject to shear strains. If soil expands its volume, the density of particles will decrease and the strength will decrease; in this case, the peak strength would be followed by a reduction of shear stress. The stress-strain relationship levels off when the material stops expanding or contracting, and when interparticle bonds are broken. The theoretical state at which the shear stress and density remain constant while the shear strain increases may be called the critical state, steady state, or residual strength.
This is an alphabetical list of articles pertaining specifically to civil engineering. For a broad overview of engineering, please see List of engineering topics. For biographies please see List of civil engineers.
The material point method (MPM) is a numerical technique used to simulate the behavior of solids, liquids, gases, and any other continuum material. Especially, it is a robust spatial discretization method for simulating multi-phase (solid-fluid-gas) interactions. In the MPM, a continuum body is described by a number of small Lagrangian elements referred to as 'material points'. These material points are surrounded by a background mesh/grid that is used only to calculate gradient terms such as the deformation gradient. Unlike other mesh-based methods like the finite element method, finite volume method or finite difference method, the MPM is not a mesh based method and is instead categorized as a meshless/meshfree or continuum-based particle method, examples of which are smoothed particle hydrodynamics and peridynamics. Despite the presence of a background mesh, the MPM does not encounter the drawbacks of mesh-based methods which makes it a promising and powerful tool in computational mechanics.

Fault gouge is a tectonite with a very small grain size. Fault gouge has no cohesion and it is normally an unconsolidated rock type, unless cementation took place at a later stage. A fault gouge forms in the same way as fault breccia, the latter also having larger clasts. In comparison to fault breccia, which is another incohesive fault rock, fault gouge has a lower volume-fraction of visible fragments. Fault gouge is also classified as have particles that are smaller than 1mm in diameter. Therefore, fault gouge is commonly composed of clays which commonly consist of Illite, Montmorillonite, Saponite, Kaolinite, Vermiculite, Quartz, Chlorite, Muscovite, Biotite, and/or Feldspars.

Jamming is the physical process by which the viscosity of some mesoscopic materials, such as granular materials, glasses, foams, polymers, emulsions, and other complex fluids, increases with increasing particle density. The jamming transition has been proposed as a new type of phase transition, with similarities to a glass transition but very different from the formation of crystalline solids.
The CFD-DEM model, or Computational Fluid Dynamics / Discrete Element Method model, is a process used to model or simulate systems combining fluids with solids or particles. In CFD-DEM, the motion of discrete solids or particles phase is obtained by the Discrete Element Method (DEM) which applies Newton's laws of motion to every particle, while the flow of continuum fluid is described by the local averaged Navier–Stokes equations that can be solved using the traditional Computational Fluid Dynamics (CFD) approach. The interactions between the fluid phase and solids phase is modeled by use of Newton's third law.
A CFD-DEM model is suitable for the modeling or simulation of fluid-solids or fluid-particles systems. In a typical CFD-DEM model, the phase motion of discrete solids or particles is obtained by the Discrete Element Method (DEM) which applies Newton's laws of motion to every particle and the flow of continuum fluid is described by the local averaged Navier–Stokes equations that can be solved by the traditional Computational Fluid Dynamics (CFD). The model is first proposed by Tsuji et al. The interactions between the fluid phase and solids phase is better modeled according to Newton's third law.
Slope stability analysis is a static or dynamic, analytical or empirical method to evaluate the stability of earth and rock-fill dams, embankments, excavated slopes, and natural slopes in soil and rock. Slope stability refers to the condition of inclined soil or rock slopes to withstand or undergo movement. The stability condition of slopes is a subject of study and research in soil mechanics, geotechnical engineering and engineering geology. Analyses are generally aimed at understanding the causes of an occurred slope failure, or the factors that can potentially trigger a slope movement, resulting in a landslide, as well as at preventing the initiation of such movement, slowing it down or arresting it through mitigation countermeasures.
Formability is the ability of a given metal workpiece to undergo plastic deformation without being damaged. The plastic deformation capacity of metallic materials, however, is limited to a certain extent, at which point, the material could experience tearing or fracture (breakage).

Lubachevsky-Stillinger (compression) algorithm is a numerical procedure suggested by F. H. Stillinger and B.D. Lubachevsky that simulates or imitates a physical process of compressing an assembly of hard particles. As the LSA may need thousands of arithmetic operations even for a few particles, it is usually carried out on a computer.
Modelling of particle breakage is a process used in grinding.
The Inertial number quantifies the significance of dynamic effects in a granular material. It measures the ratio of inertial forces of grains to imposed forces: a small value corresponds to the quasi-static state, while a high value corresponds to the inertial state or even the "dynamic" state.
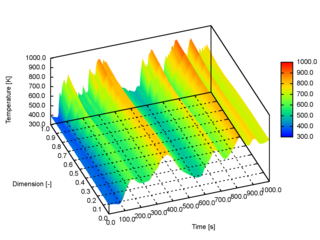
The extended discrete element method (XDEM) is a numerical technique that extends the dynamics of granular material or particles as described through the classical discrete element method (DEM) by additional properties such as the thermodynamic state, stress/strain or electro-magnetic field for each particle. Contrary to a continuum mechanics concept, the XDEM aims at resolving the particulate phase with its various processes attached to the particles. While the discrete element method predicts position and orientation in space and time for each particle, the extended discrete element method additionally estimates properties such as internal temperature and/or species distribution or mechanical impact with structures.
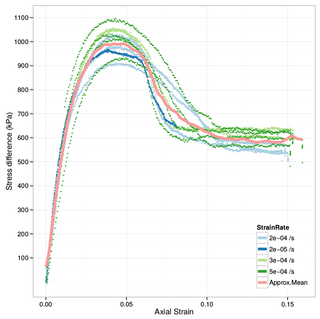
Dilatancy is the volume change observed in granular materials when they are subjected to shear deformations. This effect was first described scientifically by Osborne Reynolds in 1885/1886 and is also known as Reynolds dilatancy.
Peter Alan Cundall is an engineer and one of the founders of the Itasca Consulting Group. Together with Otto D. L. Strack, he introduced the Discrete Element Method.
References
- ↑ Cundall, P.A. and O.D.L. Strack, Discrete Numerical-Model for Granular Assemblies. Geotechnique, 1979. 29(1): p. 47–65.
- ↑ H. J. Herrmann, J.-P.H., and S. Luding., Physics of dry granular media - NATO ASI Series E 350. 1998, Dordrecht: Kluwer Acad. Publ.
- ↑ P. A. Vermeer, S.D., W. Ehlers, H. J. Herrmann, S. Luding, and E. Ramm., Continuous and Discontinuous Modelling of Cohesive Frictional Materials. 2001, Berlin: Springer.
- ↑ Oda, M. and H. Kazama, Microstructure of shear bands and its relation to the mechanisms of dilatancy and failure of dense granular soils. Geotechnique, 1998. 48(4): p. 465–481.
- ↑ Thornton, C., Numerical simulations of deviatoric shear deformation of granular media. Geotechnique, 2000. 50(1): p. 43–53.