Bra–ket notation, also called Dirac notation, is a notation for linear algebra and linear operators on complex vector spaces together with their dual space both in the finite-dimensional and infinite-dimensional case. It is specifically designed to ease the types of calculations that frequently come up in quantum mechanics. Its use in quantum mechanics is quite widespread.
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. The determinant of a matrix A is commonly denoted det(A), det A, or |A|. Its value characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants (which follows directly from the above properties).

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.
In mathematics, the tensor product of two vector spaces V and W is a vector space to which is associated a bilinear map that maps a pair to an element of denoted
In linear algebra, the outer product of two coordinate vectors is the matrix whose entries are all products of an element in the first vector with an element in the second vector. If the two coordinate vectors have dimensions n and m, then their outer product is an n × m matrix. More generally, given two tensors, their outer product is a tensor. The outer product of tensors is also referred to as their tensor product, and can be used to define the tensor algebra.

In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together.

In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.

In mathematics, the special unitary group of degree n, denoted SU(n), is the Lie group of n × n unitary matrices with determinant 1.
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group.
In quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan. The quantum operation formalism describes not only unitary time evolution or symmetry transformations of isolated systems, but also the effects of measurement and transient interactions with an environment. In the context of quantum computation, a quantum operation is called a quantum channel.
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function. The partial trace has applications in quantum information and decoherence which is relevant for quantum measurement and thereby to the decoherent approaches to interpretations of quantum mechanics, including consistent histories and the relative state interpretation.
In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers that describes the vector in terms of a particular ordered basis. An easy example may be a position such as in a 3-dimensional Cartesian coordinate system with the basis as the axes of this system. Coordinates are always specified relative to an ordered basis. Bases and their associated coordinate representations let one realize vector spaces and linear transformations concretely as column vectors, row vectors, and matrices; hence, they are useful in calculations.
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit. An example of classical information is a text document transmitted over the Internet.
In linear algebra, a nilpotent matrix is a square matrix N such that
In mathematics, a unipotent elementr of a ring R is one such that r − 1 is a nilpotent element; in other words, (r − 1)n is zero for some n.
In mathematics, a logarithm of a matrix is another matrix such that the matrix exponential of the latter matrix equals the original matrix. It is thus a generalization of the scalar logarithm and in some sense an inverse function of the matrix exponential. Not all matrices have a logarithm and those matrices that do have a logarithm may have more than one logarithm. The study of logarithms of matrices leads to Lie theory since when a matrix has a logarithm then it is in an element of a Lie group and the logarithm is the corresponding element of the vector space of the Lie algebra.
In numerical linear algebra, the method of successive over-relaxation (SOR) is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process.
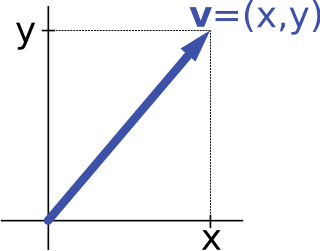
In mathematics and physics, vector notation is a commonly used notation for representing vectors, which may be Euclidean vectors, or more generally, members of a vector space.

In mathematics, the classical groups are defined as the special linear groups over the reals R, the complex numbers C and the quaternions H together with special automorphism groups of symmetric or skew-symmetric bilinear forms and Hermitian or skew-Hermitian sesquilinear forms defined on real, complex and quaternionic finite-dimensional vector spaces. Of these, the complex classical Lie groups are four infinite families of Lie groups that together with the exceptional groups exhaust the classification of simple Lie groups. The compact classical groups are compact real forms of the complex classical groups. The finite analogues of the classical groups are the classical groups of Lie type. The term "classical group" was coined by Hermann Weyl, it being the title of his 1939 monograph The Classical Groups.