A Compton generator [1] [2] or Compton tube [3] is an apparatus for experiment to demonstrate the Earth's rotation, similar to the Foucault pendulum and to gyroscope devices. [4] Arthur Compton (Nobel Prize in Physics in 1927) published it during his fourth year at the College of Wooster in 1913. [5]
A Compton generator is a circular hollow glass ring tube shaped like a doughnut, the inside of which is filled with water. [1] If the ring lies flat on the table, the water in the ring is stationary, and it is then turned over by rotating itself 180 degree around a diameter, such that it again lies flat on the table surface, which is horizontal. The result of the experiment is that the water moves with a certain constant drift velocity around the tube after the doughnut has been rotated. If there were no friction with the walls, the water would continue to circulate indefinitely. [1]
The ring used in the initial experiment was made of one inch brass tubing bent into a circle eighteen inches in diameter, where the windows were placed the tube was constricted to a diameter of about 3/8 inches (9.5 mm). [6]
Compton used small droplets of coal oil mixed in the water to measure the drift velocity under a microscope. [7]
Assume the diameter of the glass tube is much smaller than the diameter of the ring, and is the radius of the ring, is the Earth rotation rate and is the latitude.
Initially the ring is horizontal and the water is stationary. Second the ring is then quickly rotated by 180° around its East-West diameter and stopped, such that it again lies flat on the table surface, which is horizontal. At this time, the velocity of the water in the tube is given by
Note that a rotation from the vertical to the vertical position produces the velocity of the water in the tube is given by
This is derived by first integrating the torque due to the Coriolis force around the ring, then integrating the torque over the time it takes for the ring to flip, to obtain the change in angular momentum. [4]
With these two equations, one can solve for both , thus finding both the rotation speed of earth and the latitude of the apparatus.
Compton used this measured drift velocity to determine his latitude to within 3% accuracy. [7] He also used it to measure the rotational period of earth to an accuracy of 16 minutes per day (accuracy of 1%). By careful methods he could observe the effect in a ring with a radius of only 9 inches (23 cm). [8]
Earth's rotation is 7.3 × 10−5 radians/second. In the original report, Compton used a ring of 1 meter in radius at the College of Wooster (latitude 41 degrees). This would translate to a velocity of about .
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the modulation or envelope of the wave—propagates through space.
In physics, angular velocity, also known as angular frequency vector, is a pseudovector representation of how the angular position or orientation of an object changes with time, i.e. how quickly an object rotates around an axis of rotation and how fast the axis itself changes direction.
In fluid dynamics, a vortex is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in the wake of a boat, and the winds surrounding a tropical cyclone, tornado or dust devil.
Differential rotation is seen when different parts of a rotating object move with different angular velocities at different latitudes and/or depths of the body and/or in time. This indicates that the object is not rigid. In fluid objects, such as accretion disks, this leads to shearing. Galaxies and protostars usually show differential rotation; examples in the Solar System include the Sun, Jupiter and Saturn.
The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
A vortex ring, also called a toroidal vortex, is a torus-shaped vortex in a fluid; that is, a region where the fluid mostly spins around an imaginary axis line that forms a closed loop. The dominant flow in a vortex ring is said to be toroidal, more precisely poloidal.
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the dispersion relation, one can calculate the frequency-dependent phase velocity and group velocity of each sinusoidal component of a wave in the medium, as a function of frequency. In addition to the geometry-dependent and material-dependent dispersion relations, the overarching Kramers–Kronig relations describe the frequency-dependence of wave propagation and attenuation.
The Sagnac effect, also called Sagnac interference, named after French physicist Georges Sagnac, is a phenomenon encountered in interferometry that is elicited by rotation. The Sagnac effect manifests itself in a setup called a ring interferometer or Sagnac interferometer. A beam of light is split and the two beams are made to follow the same path but in opposite directions. On return to the point of entry the two light beams are allowed to exit the ring and undergo interference. The relative phases of the two exiting beams, and thus the position of the interference fringes, are shifted according to the angular velocity of the apparatus. In other words, when the interferometer is at rest with respect to a nonrotating frame, the light takes the same amount of time to traverse the ring in either direction. However, when the interferometer system is spun, one beam of light has a longer path to travel than the other in order to complete one circuit of the mechanical frame, and so takes longer, resulting in a phase difference between the two beams. Georges Sagnac set up this experiment in an attempt to prove the existence of the aether that Einstein's theory of special relativity had discarded.
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, with gravity and surface tension as the restoring forces. As a result, water with a free surface is generally considered to be a dispersive medium.
Greek letters are used in mathematics, science, engineering, and other areas where mathematical notation is used as symbols for constants, special functions, and also conventionally for variables representing certain quantities. In these contexts, the capital letters and the small letters represent distinct and unrelated entities. Those Greek letters which have the same form as Latin letters are rarely used: capital A, B, E, Z, H, I, K, M, N, O, P, T, Y, X. Small ι, ο and υ are also rarely used, since they closely resemble the Latin letters i, o and u. Sometimes, font variants of Greek letters are used as distinct symbols in mathematics, in particular for ε/ϵ and π/ϖ. The archaic letter digamma (Ϝ/ϝ/ϛ) is sometimes used.
The Michelson–Gale–Pearson experiment (1925) is a modified version of the Michelson–Morley experiment and the Sagnac-Interferometer. It measured the Sagnac effect due to Earth's rotation, and thus tests the theories of special relativity and luminiferous ether along the rotating frame of Earth.
The Coriolis frequencyƒ, also called the Coriolis parameter or Coriolis coefficient, is equal to twice the rotation rate Ω of the Earth multiplied by the sine of the latitude .
The Eötvös effect is the change in measured Earth's gravity caused by the change in centrifugal acceleration resulting from eastbound or westbound velocity. When moving eastbound, the object's angular velocity is increased, and thus the centrifugal force also increases, causing a perceived reduction in gravitational force.
In classical mechanics, the Hannay angle is a mechanics analogue of the whirling geometric phase. It was named after John Hannay of the University of Bristol, UK. Hannay first described the angle in 1985, extending the ideas of the recently formalized Berry phase to classical mechanics.
Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly observable, but is more convenient for calculations. The distance measures discussed here all reduce to the common notion of Euclidean distance at low redshift.
For a pure wave motion in fluid dynamics, the Stokes drift velocity is the average velocity when following a specific fluid parcel as it travels with the fluid flow. For instance, a particle floating at the free surface of water waves, experiences a net Stokes drift velocity in the direction of wave propagation.
Polflucht is a geophysical concept invoked in 1922 by Alfred Wegener to explain his ideas of continental drift.
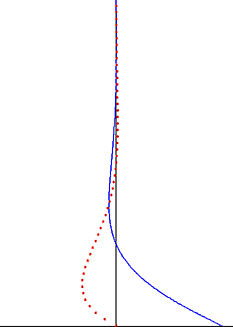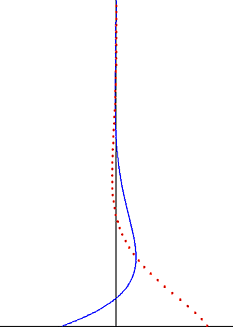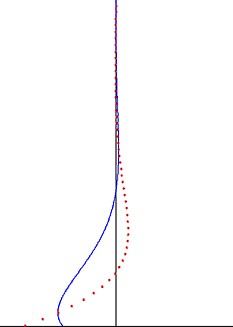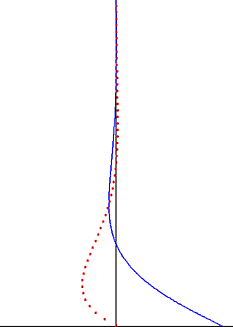
In fluid dynamics, Stokes problem also known as Stokes second problem or sometimes referred to as Stokes boundary layer or Oscillating boundary layer is a problem of determining the flow created by an oscillating solid surface, named after Sir George Stokes. This is considered one of the simplest unsteady problems that has an exact solution for the Navier-Stokes equations. In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments, numerical simulations or approximate methods in order to obtain useful information on the flow.
The Gibbs rotational ensemble represents the possible states of a mechanical system in thermal and rotational equilibrium at temperature and angular velocity . The Jaynes procedure can be used to obtain this ensemble. An ensemble is the set of microstates corresponding to a given macrostate.
