In mathematics, a conchospiral a specific type of space spiral on the surface of a cone (a conical spiral ), whose floor projection is a logarithmic spiral. Conchospirals are used in biology for modelling snail shells, and flight paths of insects [1] [2] and in electrical engineering for the construction of antennas. [3] [4]
In cylindrical coordinates, the conchospiral is described by the parametric equations:
The projection of a conchospiral on the plane is a logarithmic spiral. The parameter controls the opening angle of the projected spiral, while the parameter controls the slope of the cone on which the curve lies.
The name "conchospiral" was given to these curves by 19th-century German mineralogist Georg Amadeus Carl Friedrich Naumann, in his study of the shapes of sea shells. [5]
The conchospiral has been used in the design for radio antennas. In this application, it has the advantage of producing a radio beam in a single direction, towards the apex of the cone. [6] [7]
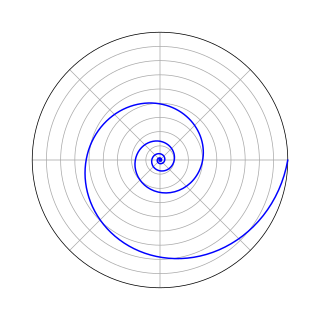
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral curve that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer (1525) who called it an "eternal line". More than a century later, the curve was discussed by Descartes (1638), and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous spiral".
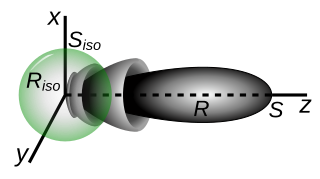
In electromagnetics, an antenna's gain is a key performance parameter which combines the antenna's directivity and radiation efficiency. The term power gain has been deprecated by IEEE. In a transmitting antenna, the gain describes how well the antenna converts input power into radio waves headed in a specified direction. In a receiving antenna, the gain describes how well the antenna converts radio waves arriving from a specified direction into electrical power. When no direction is specified, gain is understood to refer to the peak value of the gain, the gain in the direction of the antenna's main lobe. A plot of the gain as a function of direction is called the antenna pattern or radiation pattern. It is not to be confused with directivity, which does not take an antenna's radiation efficiency into account.
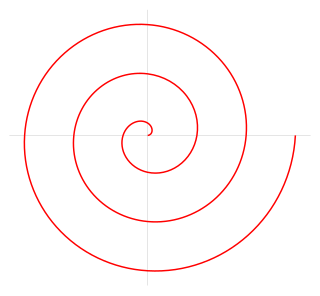
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.
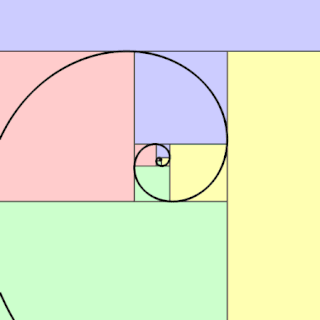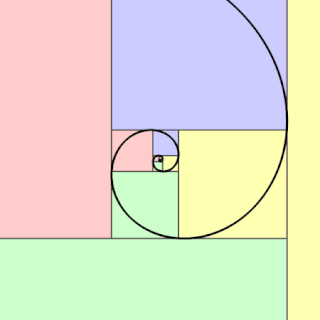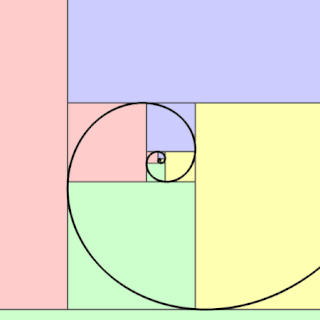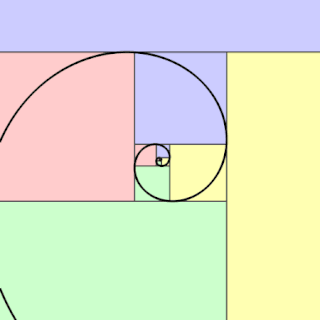
In geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio. That is, a golden spiral gets wider by a factor of φ for every quarter turn it makes.
In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz.
In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.
The angle of repose, or critical angle of repose, of a granular material is the steepest angle of descent or dip relative to the horizontal plane to which the material can be piled without slumping. At this angle, the material on the slope face is on the verge of sliding. The angle of repose can range from 0° to 90°. The morphology of the material affects the angle of repose; smooth, rounded sand grains cannot be piled as steeply as can rough, interlocking sands. The angle of repose can also be affected by additions of solvents. If a small amount of water is able to bridge the gaps between particles, electrostatic attraction of the water to mineral surfaces will increase the angle of repose, and related quantities such as the soil strength.
In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.
In probability theory, the Rice distribution or Rician distribution is the probability distribution of the magnitude of a circularly-symmetric bivariate normal random variable, possibly with non-zero mean (noncentral). It was named after Stephen O. Rice (1907–1986).
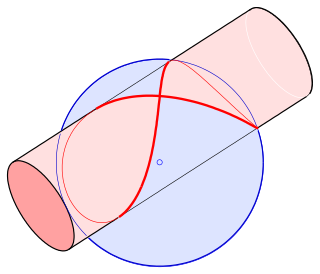
In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles of the sphere. Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.
Antenna measurement techniques refers to the testing of antennas to ensure that the antenna meets specifications or simply to characterize it. Typical parameters of antennas are gain, bandwidth, radiation pattern, beamwidth, polarization, and impedance.
In the mathematical theory of bifurcations, a Hopfbifurcation is a critical point where a system's stability switches and a periodic solution arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system loses stability, as a pair of complex conjugate eigenvalues—of the linearization around the fixed point—crosses the complex plane imaginary axis. Under reasonably generic assumptions about the dynamical system, a small-amplitude limit cycle branches from the fixed point.
In probability theory and directional statistics, a wrapped normal distribution is a wrapped probability distribution that results from the "wrapping" of the normal distribution around the unit circle. It finds application in the theory of Brownian motion and is a solution to the heat equation for periodic boundary conditions. It is closely approximated by the von Mises distribution, which, due to its mathematical simplicity and tractability, is the most commonly used distribution in directional statistics.
In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution.
In probability theory and directional statistics, a wrapped Lévy distribution is a wrapped probability distribution that results from the "wrapping" of the Lévy distribution around the unit circle.
In microwave systems, a spiral antenna is a type of RF antenna. It is shaped as a two-arm spiral, or more arms may be used. Spiral antennas were first described in 1956. Logarithmic spiral antennas belong to the class of frequency independent antennas; the driving point impedance, radiation pattern and polarization of such antennas remain unchanged over a large bandwidth range. Spiral antennas are inherently circularly polarized with low gain. Antenna arrays can be used to increase the gain. Spiral antennas are reduced size antennas with its windings making it an extremely small structure. Lossy cavities are usually placed at the back to eliminate back lobes because a unidirectional pattern is usually preferred in such antennas. Spiral antennas are classified into different types; Archimedean spiral, logarithmic spiral, square spiral, and star spiral, etc. Archimedean spiral is the most popular configuration.
In statistics, the variance function is a smooth function which depicts the variance of a random quantity as a function of its mean. The variance function is a measure of heteroscedasticity and plays a large role in many settings of statistical modelling. It is a main ingredient in the generalized linear model framework and a tool used in non-parametric regression, semiparametric regression and functional data analysis. In parametric modeling, variance functions take on a parametric form and explicitly describe the relationship between the variance and the mean of a random quantity. In a non-parametric setting, the variance function is assumed to be a smooth function.
X-ray computed tomography operates by using an X-ray generator that rotates around the object; X-ray detectors are positioned on the opposite side of the circle from the X-ray source.
In mathematics, a conical spiral, also known as a conical helix, is a space curve on a right circular cone, whose floor plan is a plane spiral. If the floor plan is a logarithmic spiral, it is called conchospiral.
