In formal language theory, a context-sensitive language is a language that can be defined by a context-sensitive grammar. Context-sensitive is one of the four types of grammars in the Chomsky hierarchy.

In logic, mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules.

In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.
In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
Sheila Adele Greibach is a researcher in formal languages in computing, automata, compiler theory and computer science. She is an Emeritus Professor of Computer Science at the University of California, Los Angeles, and notable work include working with Seymour Ginsburg and Michael A. Harrison in context-sensitive parsing using the stack automaton model.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines relations between sets of strings.
In theoretical computer science and mathematical logic a string rewriting system (SRS), historically called a semi-Thue system, is a rewriting system over strings from a alphabet. Given a binary relation between fixed strings over the alphabet, called rewrite rules, denoted by , an SRS extends the rewriting relation to all strings in which the left- and right-hand side of the rules appear as substrings, that is , where , , , and are strings.
Conjunctive grammars are a class of formal grammars studied in formal language theory. They extend the basic type of grammars, the context-free grammars, with a conjunction operation. Besides explicit conjunction, conjunctive grammars allow implicit disjunction represented by multiple rules for a single nonterminal symbol, which is the only logical connective expressible in context-free grammars. Conjunction can be used, in particular, to specify intersection of languages. A further extension of conjunctive grammars known as Boolean grammars additionally allows explicit negation.
In formal language theory, an alphabet is a non-empty set of symbols/glyphs, typically thought of as representing letters, characters, or digits but among other possibilities the "symbols" could also be a set of phonemes. Alphabets in this technical sense of a set are used in a diverse range of fields including logic, mathematics, computer science, and linguistics. An alphabet may have any cardinality ("size") and depending on its purpose maybe be finite, countable, or even uncountable.
Language equations are mathematical statements that resemble numerical equations, but the variables assume values of formal languages rather than numbers. Instead of arithmetic operations in numerical equations, the variables are joined by language operations. Among the most common operations on two languages A and B are the set union A ∪ B, the set intersection A ∩ B, and the concatenation A⋅B. Finally, as an operation taking a single operand, the set A* denotes the Kleene star of the language A. Therefore language equations can be used to represent formal grammars, since the languages generated by the grammar must be the solution of a system of language equations.
In computer science, in the area of formal language theory, frequent use is made of a variety of string functions; however, the notation used is different from that used for computer programming, and some commonly used functions in the theoretical realm are rarely used when programming. This article defines some of these basic terms.
In computer science, in particular in the field of formal language theory, an abstract family of languages is an abstract mathematical notion generalizing characteristics common to the regular languages, the context-free languages and the recursively enumerable languages, and other families of formal languages studied in the scientific literature.
An abstract family of acceptors (AFA) is a grouping of generalized acceptors. Informally, an acceptor is a device with a finite state control, a finite number of input symbols, and an internal store with a read and write function. Each acceptor has a start state and a set of accepting states. The device reads a sequence of symbols, transitioning from state to state for each input symbol. If the device ends in an accepting state, the device is said to accept the sequence of symbols. A family of acceptors is a set of acceptors with the same type of internal store. The study of AFA is part of AFL (abstract families of languages) theory.
In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.
In automata theory, a timed automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a timed automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Timed automata are a sub-class of a type hybrid automata.
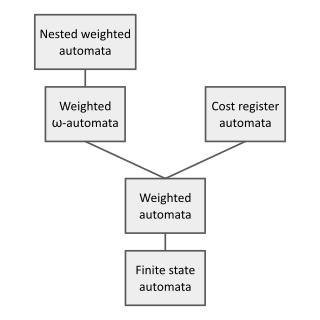
In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.
In formal language theory, the Chomsky–Schützenberger representation theorem is a theorem derived by Noam Chomsky and Marcel-Paul Schützenberger about representing a given context-free language in terms of two simpler languages. These two simpler languages, namely a regular language and a Dyck language, are combined by means of an intersection and a homomorphism.
In mathematics, the Muller–Schupp theorem states that a finitely generated group G has context-free word problem if and only if G is virtually free. The theorem was proved by David Muller and Paul Schupp in 1983.




















