Related Research Articles

In mathematics, specifically abstract algebra, an integral domain is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. Integral domains are generalizations of the ring of integers and provide a natural setting for studying divisibility. In an integral domain, every nonzero element a has the cancellation property, that is, if a ≠ 0, an equality ab = ac implies b = c.

In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being 0.

In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative internal binary operation on it.

In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. In other words, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.
In mathematics, more specifically ring theory, the Jacobson radical of a ring is the ideal consisting of those elements in that annihilate all simple right -modules. It happens that substituting "left" in place of "right" in the definition yields the same ideal, and so the notion is left-right symmetric. The Jacobson radical of a ring is frequently denoted by or ; the former notation will be preferred in this article, because it avoids confusion with other radicals of a ring. The Jacobson radical is named after Nathan Jacobson, who was the first to study it for arbitrary rings in.
In mathematics, the endomorphisms of an abelian group X form a ring. This ring is called the endomorphism ring of X, denoted by End(X); the set of all homomorphisms of X into itself. Addition of endomorphisms arises naturally in a pointwise manner and multiplication via endomorphism composition. Using these operations, the set of endomorphisms of an abelian group forms a (unital) ring, with the zero map as additive identity and the identity map as multiplicative identity.

In mathematics, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra. Complementarily, noncommutative algebra is the study of ring properties that are not specific to commutative rings. This distinction results from the high number of fundamental properties of commutative rings that do not extend to noncommutative rings.

In algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those operations defined for the integers. Ring theory studies the structure of rings, their representations, or, in different language, modules, special classes of rings, as well as an array of properties that proved to be of interest both within the theory itself and for its applications, such as homological properties and polynomial identities.
Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject.
In mathematics, an element of a ring is called nilpotent if there exists some positive integer , called the index, such that .
In mathematics, and more specifically in abstract algebra, a *-algebra is a mathematical structure consisting of two involutive ringsR and A, where R is commutative and A has the structure of an associative algebra over R. Involutive algebras generalize the idea of a number system equipped with conjugation, for example the complex numbers and complex conjugation, matrices over the complex numbers and conjugate transpose, and linear operators over a Hilbert space and Hermitian adjoints. However, it may happen that an algebra admits no involution.
In ring theory, a branch of mathematics, an idempotent element or simply idempotent of a ring is an element a such that a2 = a. That is, the element is idempotent under the ring's multiplication. Inductively then, one can also conclude that a = a2 = a3 = a4 = ... = an for any positive integer n. For example, an idempotent element of a matrix ring is precisely an idempotent matrix.

In abstract algebra, a semiring is an algebraic structure. It is a generalization of a ring, dropping the requirement that each element must have an additive inverse. At the same time, it is a generalization of bounded distributive lattices.
In ring theory and related areas of mathematics a central simple algebra (CSA) over a field K is a finite-dimensional associative K-algebraA which is simple, and for which the center is exactly K.
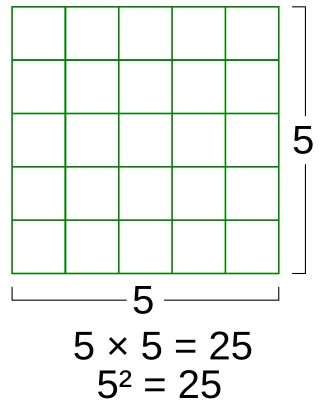
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x2. The adjective which corresponds to squaring is quadratic.
In mathematics, a von Neumann regular ring is a ring R such that for every element a in R there exists an x in R with a = axa. One may think of x as a "weak inverse" of the element a; in general x is not uniquely determined by a. Von Neumann regular rings are also called absolutely flat rings, because these rings are characterized by the fact that every left R-module is flat.
In mathematics, and more specifically in abstract algebra, a rng is an algebraic structure satisfying the same properties as a ring, but without assuming the existence of a multiplicative identity. The term rng is meant to suggest that it is a ring without i, that is, without the requirement for an identity element.
In mathematics, especially in the field of ring theory, the term irreducible ring is used in a few different ways.
In mathematics, more specifically abstract algebra, a finite ring is a ring that has a finite number of elements. Every finite field is an example of a finite ring, and the additive part of every finite ring is an example of an abelian finite group, but the concept of finite rings in their own right has a more recent history.

In mathematics, a noncommutative ring is a ring whose multiplication is not commutative; that is, there exist a and b in the ring such that ab and ba are different. Equivalently, a noncommutative ring is a ring that is not a commutative ring.
References
- ↑ Jacobson 1989, p 418.
- Jacobson, Nathan (1989), Basic algebra. II (2 ed.), New York: W. H. Freeman and Company, pp. xviii+686, ISBN 0-7167-1933-9, MR 1009787
