Constructive function theory

Last updated

In mathematical analysis, constructive function theory is a field which studies the connection between the smoothness of a function and its degree of approximation. [1] [2] It is closely related to approximation theory. The term was coined by Sergei Bernstein.

Mathematical analysis branch of pure mathematics

Mathematical analysis is the branch of mathematics dealing with limits and related theories, such as differentiation, integration, measure, infinite series, and analytic functions.

Function (mathematics) Mathematical binary relation

In mathematics, a function was originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a function of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable. The concept of function was formalized at the end of the 19th century in terms of set theory, and this greatly enlarged the domains of application of the concept.

Approximation theory Theory of getting acceptably close inexact mathematical calculations

In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby. Note that what is meant by best and simpler will depend on the application.

Contents

Example

Let f be a 2π-periodic function. Then f is α-Hölder for some 0 < α < 1 if and only if for every natural n there exists a trigonometric polynomial Pn of degree n such that

In mathematics, a real or complex-valued function f on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, α>0, such that

In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin(nx) and cos(nx) with n taking on the values of one or more natural numbers. The coefficients may be taken as real numbers, for real-valued functions. For complex coefficients, there is no difference between such a function and a finite Fourier series.

where C(f) is a positive number depending on f. The "only if" is due to Dunham Jackson, see Jackson's inequality; the "if" part is due to Sergei Bernstein, see Bernstein's theorem (approximation theory).

Dunham Jackson was a mathematician who worked within approximation theory, notably with trigonometrical and orthogonal polynomials. He is known for Jackson's inequality. He was awarded the Chauvenet Prize in 1935. His book Fourier Series and Orthogonal Polynomials was reprinted in 2004.

In approximation theory, Jackson's inequality is an inequality bounding the value of function's best approximation by algebraic or trigonometric polynomials in terms of the modulus of continuity or modulus of smoothness of the function or of its derivatives. Informally speaking, the smoother the function is, the better it can be approximated by polynomials.

In approximation theory, Bernstein's theorem is a converse to Jackson's theorem. The first results of this type were proved by Sergei Bernstein in 1912.

Notes

  1. ↑ "Constructive Theory of Functions".
  2. ↑ Telyakovskii, S.A. (2001) [1994], "Constructive theory of functions", in Hazewinkel, Michiel, Encyclopedia of Mathematics , Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN   978-1-55608-010-4

Related Research Articles

Dirac delta function pseudo-function δ such that an integral of δ(x-c)f(x) always takes the value of f(c)

In mathematics, the Dirac delta function is a generalized function or distribution introduced by the physicist Paul Dirac. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by the theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.

In mathematics, the Weil conjectures were some highly influential proposals by André Weil (1949), which led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.

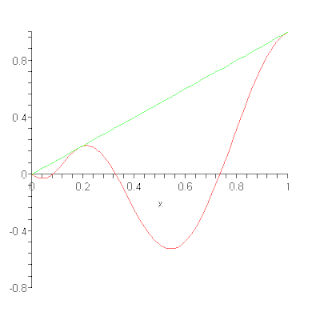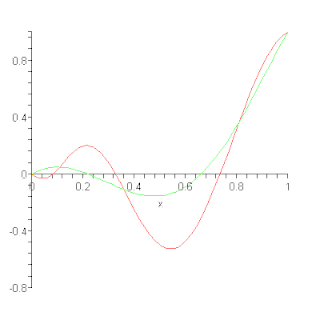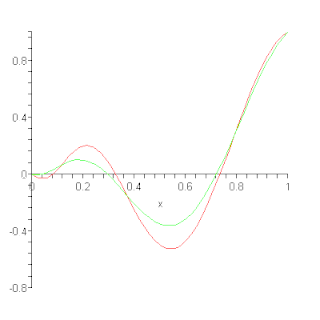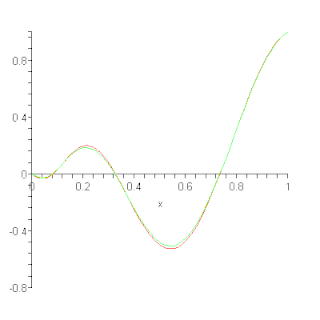
Bernstein polynomial

In the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials.

Sergei Natanovich Bernstein Russian mathematician

Sergei Natanovich Bernstein was a Russian and Soviet mathematician of Jewish origin known for contributions to partial differential equations, differential geometry, probability theory, and approximation theory.

In mathematics, a sequence {s1, s2, s3, ...} of real numbers is said to be equidistributed, or uniformly distributed, if the proportion of terms falling in a subinterval is proportional to the length of that interval. Such sequences are studied in Diophantine approximation theory and have applications to Monte Carlo integration.

In mathematical analysis, Bernstein's inequality is named after Sergei Natanovich Bernstein. The inequality states that on the complex plane, within the disk of radius 1, the degree of a polynomial times the maximum value of a polynomial is an upper bound for the similar maximum of its derivative.

The Remez algorithm or Remez exchange algorithm, published by Evgeny Yakovlevich Remez in 1934, is an iterative algorithm used to find simple approximations to functions, specifically, approximations by functions in a Chebyshev space that are the best in the uniform norm L∞ sense.

In mathematics, the Riesz potential is a potential named after its discoverer, the Hungarian mathematician Marcel Riesz. In a sense, the Riesz potential defines an inverse for a power of the Laplace operator on Euclidean space. They generalize to several variables the Riemann–Liouville integrals of one variable.

In mathematics, the Markov brothers' inequality is an inequality proved in the 1890s by brothers Andrey Markov and Vladimir Markov, two Russian mathematicians. This inequality bounds the maximum of the derivatives of a polynomial on an interval in terms of the maximum of the polynomial. For k = 1 it was proved by Andrey Markov, and for k = 2,3,... by his brother Vladimir Markov.

In mathematics, the ATS theorem is the theorem on the approximation of a trigonometric sum by a shorter one. The application of the ATS theorem in certain problems of mathematical and theoretical physics can be very helpful.

In mathematics, a submodular set function is a set function whose value, informally, has the property that the difference in the incremental value of the function that a single element makes when added to an input set decreases as the size of the input set increases. Submodular functions have a natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory and electrical networks. Recently, submodular functions have also found immense utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains.

Nikolai Maximovich Günther was a Russian mathematician known for his work in potential theory and in integral and partial differential equations: later studies have uncovered his contributions to the theory of Gröbner bases.

In mathematics, moduli of smoothness are used to quantitatively measure smoothness of functions. Moduli of smoothness generalise modulus of continuity and are used in approximation theory and numerical analysis to estimate errors of approximation by polynomials and splines.

References

Naum Akhiezer Russian mathematician

Naum Ilyich Akhiezer was a Soviet mathematician of Jewish origin, known for his works in approximation theory and the theory of differential and integral operators. He is also known as the author of classical books on various subjects in analysis, and for his work on the history of mathematics. He is the brother of the theoretical physicist Aleksander Akhiezer.

Isidor Pavlovich Natanson was a Swiss-born Soviet mathematician known for contributions to real analysis and constructive function theory, in particular, for his textbooks on these subjects. His son, Garal'd Natanson (1930–2003), was also a known mathematician.

Mathematical Reviews is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also publishes an associated online bibliographic database called MathSciNet which contains an electronic version of Mathematical Reviews and additionally contains citation information for over 3.5 million items as of 2018.

Natanson, I. P. (1965). Constructive function theory. Vol. II. Approximation in mean. New York: Frederick Ungar Publishing Co. MR   0196341. 
Natanson, I. P. (1965). Constructive function theory. Vol. III. Interpolation and approximation quadratures. New York: Ungar Publishing Co. MR   0196342. 
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.