
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items. The problem often arises in resource allocation where the decision makers have to choose from a set of non-divisible projects or tasks under a fixed budget or time constraint, respectively.

Linear programming is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming.

Mathematical optimization or mathematical programming is the selection of a best element from some set of available alternatives. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
In computer science and optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the total weight of the edges in the minimum cut, i.e. the smallest total weight of the edges which if removed would disconnect the source from the sink.
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows:
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints are linear.

In operations research, applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not tractable. It operates on the domain of those optimization problems in which the set of feasible solutions is discrete or can be reduced to discrete, and in which the goal is to find the best solution. Some common problems involving combinatorial optimization are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem.

In mathematical optimization, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed cuts. Such procedures are commonly used to find integer solutions to mixed integer linear programming (MILP) problems, as well as to solve general, not necessarily differentiable convex optimization problems. The use of cutting planes to solve MILP was introduced by Ralph E. Gomory.
In computational complexity theory, a numeric algorithm runs in pseudo-polynomial time if its running time is a polynomial in the numeric value of the input — but not necessarily in the length of the input, which is the case for polynomial time algorithms.
In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. The solution to the dual problem provides a lower bound to the solution of the primal (minimization) problem. However in general the optimal values of the primal and dual problems need not be equal. Their difference is called the duality gap. For convex optimization problems, the duality gap is zero under a constraint qualification condition.
Semidefinite programming (SDP) is a subfield of convex optimization concerned with the optimization of a linear objective function over the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron.

In mathematics, the relaxation of a (mixed) integer linear program is the problem that arises by removing the integrality constraint of each variable.

The vehicle routing problem (VRP) is a combinatorial optimization and integer programming problem which asks "What is the optimal set of routes for a fleet of vehicles to traverse in order to deliver to a given set of customers?". It generalises the well-known travelling salesman problem (TSP). It first appeared in a paper by George Dantzig and John Ramser in 1959, in which first algorithmic approach was written and was applied to petrol deliveries. Often, the context is that of delivering goods located at a central depot to customers who have placed orders for such goods. The objective of the VRP is to minimize the total route cost. In 1964, Clarke and Wright improved on Dantzig and Ramser's approach using an effective greedy approach called the savings algorithm.
In applied mathematics, the maximum generalized assignment problem is a problem in combinatorial optimization. This problem is a generalization of the assignment problem in which both tasks and agents have a size. Moreover, the size of each task might vary from one agent to the other.
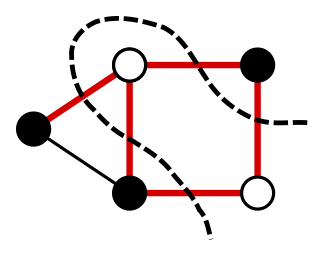
For a graph, a maximum cut is a cut whose size is at least the size of any other cut. The problem of finding a maximum cut in a graph is known as the Max-Cut Problem.
In mathematics, a submodular set function is a set function whose value, informally, has the property that the difference in the incremental value of the function that a single element makes when added to an input set decreases as the size of the input set increases. Submodular functions have a natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory and electrical networks. Recently, submodular functions have also found immense utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains.
Fisher market is an economic model attributed to Irving Fisher. It has the following ingredients:
The quadratic knapsack problem (QKP), first introduced in 19th century, is an extension of knapsack problem that allows for quadratic terms in the objective function: Given a set of items, each with a weight, a value, and an extra profit that can be earned if two items are selected, determine the number of item to include in a collection without exceeding capacity of the knapsack, so as to maximize the overall profit. Usually, quadratic knapsack problems come with a restriction on the number of copies of each kind of item: either 0, or 1. This special type of QKP forms the 0-1 quadratic knapsack problem, which was first discussed by Gallo et al. The 0-1 quadratic knapsack problem is a variation of knapsack problems, combining the features of unbounded knapsack problem, 0-1 knapsack problem and quadratic knapsack problem.
Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. The power of quantum computing may allow solving problems which are not practically feasible on classical computers, or suggest a considerable speed up with respect to the best known classical algorithm. Among other quantum algorithms, there are quantum optimization algorithms which might suggest improvement in solving optimization problems.









