Related Research Articles
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. This mathematical formalism uses mainly a part of functional analysis, especially Hilbert spaces, which are a kind of linear space. Such are distinguished from mathematical formalisms for physics theories developed prior to the early 1900s by the use of abstract mathematical structures, such as infinite-dimensional Hilbert spaces (L2 space mainly), and operators on these spaces. In brief, values of physical observables such as energy and momentum were no longer considered as values of functions on phase space, but as eigenvalues; more precisely as spectral values of linear operators in Hilbert space.

Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science.

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.
In quantum mechanics, wave function collapse occurs when a wave function—initially in a superposition of several eigenstates—reduces to a single eigenstate due to interaction with the external world. This interaction is called an "observation". It is the essence of a measurement in quantum mechanics which connects the wave function with classical observables like position and momentum. Collapse is one of two processes by which quantum systems evolve in time; the other is the continuous evolution via the Schrödinger equation. Collapse is a black box for a thermodynamically irreversible interaction with a classical environment. Calculations of quantum decoherence show that when a quantum system interacts with the environment, the superpositions apparently reduce to mixtures of classical alternatives. Significantly, the combined wave function of the system and environment continue to obey the Schrödinger equation throughout this apparent collapse. More importantly, this is not enough to explain actual wave function collapse, as decoherence does not reduce it to a single eigenstate.

A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it. The most common symbols for a wave function are the Greek letters ψ and Ψ.
A virtual particle is a transient quantum fluctuation that exhibits some of the characteristics of an ordinary particle, while having its existence limited by the uncertainty principle. The concept of virtual particles arises in perturbation theory of quantum field theory where interactions between ordinary particles are described in terms of exchanges of virtual particles. A process involving virtual particles can be described by a schematic representation known as a Feynman diagram, in which virtual particles are represented by internal lines.
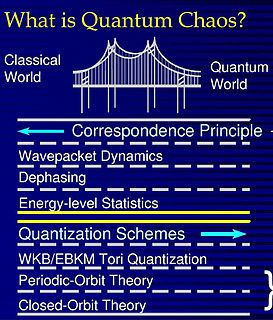
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is: "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle states that classical mechanics is the classical limit of quantum mechanics, specifically in the limit as the ratio of Planck's constant to the action of the system tends to zero. If this is true, then there must be quantum mechanisms underlying classical chaos. If quantum mechanics does not demonstrate an exponential sensitivity to initial conditions, how can exponential sensitivity to initial conditions arise in classical chaos, which must be the correspondence principle limit of quantum mechanics?
In quantum mechanics, the principal quantum number is one of four quantum numbers assigned to each electron in an atom to describe that electron's state. Its values are natural numbers making it a discrete variable.

A physical quantity is said to have a discrete spectrum if it takes only distinct values, with gaps between one value and the next.
In quantum physics, Regge theory is the study of the analytic properties of scattering as a function of angular momentum, where the angular momentum is not restricted to be an integer multiple of ħ but is allowed to take any complex value. The nonrelativistic theory was developed by Tullio Regge in 1959.
In mathematics and physics, scattering theory is a framework for studying and understanding the scattering of waves and particles. Wave scattering corresponds to the collision and scattering of a wave with some material object, for instance sunlight scattered by rain drops to form a rainbow. Scattering also includes the interaction of billiard balls on a table, the Rutherford scattering of alpha particles by gold nuclei, the Bragg scattering of electrons and X-rays by a cluster of atoms, and the inelastic scattering of a fission fragment as it traverses a thin foil. More precisely, scattering consists of the study of how solutions of partial differential equations, propagating freely "in the distant past", come together and interact with one another or with a boundary condition, and then propagate away "to the distant future". The direct scattering problem is the problem of determining the distribution of scattered radiation/particle flux basing on the characteristics of the scatterer. The inverse scattering problem is the problem of determining the characteristics of an object from measurement data of radiation or particles scattered from the object.

In quantum mechanics, an energy level is degenerate if it corresponds to two or more different measurable states of a quantum system. Conversely, two or more different states of a quantum mechanical system are said to be degenerate if they give the same value of energy upon measurement. The number of different states corresponding to a particular energy level is known as the degree of degeneracy of the level. It is represented mathematically by the Hamiltonian for the system having more than one linearly independent eigenstate with the same energy eigenvalue. When this is the case, energy alone is not enough to characterize what state the system is in, and other quantum numbers are needed to characterize the exact state when distinction is desired. In classical mechanics, this can be understood in terms of different possible trajectories corresponding to the same energy.
Quantum mechanics is the study of very small things. It explains the behavior of matter and its interactions with energy on the scale of atomic and subatomic particles. By contrast, classical physics explains matter and energy only on a scale familiar to human experience, including the behavior of astronomical bodies such as the Moon. Classical physics is still used in much of modern science and technology. However, towards the end of the 19th century, scientists discovered phenomena in both the large (macro) and the small (micro) worlds that classical physics could not explain. The desire to resolve inconsistencies between observed phenomena and classical theory led to two major revolutions in physics that created a shift in the original scientific paradigm: the theory of relativity and the development of quantum mechanics. This article describes how physicists discovered the limitations of classical physics and developed the main concepts of the quantum theory that replaced it in the early decades of the 20th century. It describes these concepts in roughly the order in which they were first discovered. For a more complete history of the subject, see History of quantum mechanics.
The Lippmann–Schwinger equation is one of the most used equations to describe particle collisions – or, more precisely, scattering – in quantum mechanics. It may be used in scattering of molecules, atoms, neutrons, photons or any other particles and is important mainly in atomic, molecular, and optical physics, nuclear physics and particle physics, but also for seismic scattering problems in geophysics. It relates the scattered wave function with the interaction that produces the scattering and therefore allows calculation of the relevant experimental parameters.
The Born rule is a key postulate of quantum mechanics which gives the probability that a measurement of a quantum system will yield a given result. In its simplest form, it states that the probability density of finding a particle at a given point, when measured, is proportional to the square of the magnitude of the particle's wavefunction at that point. It was formulated by German physicist Max Born in 1926.
Asım Orhan Barut was a Turkish-American theoretical physicist.
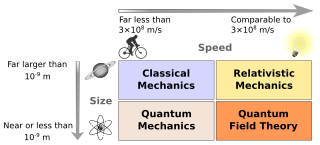
Physics is a scientific discipline that seeks to construct and experimentally test theories of the physical universe. These theories vary in their scope and can be organized into several distinct branches, which are outlined in this article.
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in time exhausts all that can be predicted about the system's behavior. A mixture of quantum states is again a quantum state. Quantum states that cannot be written as a mixture of other states are called pure quantum states, while all other states are called mixed quantum states. A pure quantum state can be represented by a ray in a Hilbert space over the complex numbers, while mixed states are represented by density matrices, which are positive semidefinite operators that act on Hilbert spaces.
This is a glossary for the terminology often encountered in undergraduate quantum mechanics courses.
This glossary of physics is a list of definitions of terms and concepts relevant to physics, its sub-disciplines, and related fields, including mechanics, materials science, nuclear physics, particle physics, and thermodynamics. For more inclusive glossaries concerning related fields of science and technology, see Glossary of chemistry terms, Glossary of astronomy, Glossary of areas of mathematics, and Glossary of engineering.
References
- ↑ Landau, L. D.; Lifshitz, E. M. (1977), Course of theoretical physics III: Quantum mechanics, Non-relativistic theory (3rd ed.), Pergamon Press, p. 121
- ↑ Mulherin, Denis. "Coulomb Scattering. I. Single Channel". Journal of Mathematical Physics. 11 (4): 1402. Bibcode:1970JMP....11.1402M. doi:10.1063/1.1665275.