Wilhelm Ostwald’s dilution law is a relationship proposed in 1888 between the dissociation constant Kd and the degree of dissociation α of a weak electrolyte. The law takes the form

A gel is a semi-solid that can have properties ranging from soft and weak to hard and tough. Gels are defined as a substantially dilute cross-linked system, which exhibits no flow when in the steady-state, although the liquid phase may still diffuse through this system. A gel has been defined phenomenologically as a soft, solid or solid-like material consisting of two or more components, one of which is a liquid, present in substantial quantity.
In plasmas and electrolytes, the Debye length, is a measure of a charge carrier's net electrostatic effect in a solution and how far its electrostatic effect persists. With each Debye length the charges are increasingly electrically screened and the electric potential decreases in magnitude by 1/e. A Debye sphere is a volume whose radius is the Debye length. Debye length is an important parameter in plasma physics, electrolytes, and colloids. The corresponding Debye screening wave vector for particles of density , charge at a temperature is given by in Gaussian units. Expressions in MKS units will be given below. The analogous quantities at very low temperatures are known as the Thomas–Fermi length and the Thomas–Fermi wave vector. They are of interest in describing the behaviour of electrons in metals at room temperature.
The DLVO theory explains the aggregation and kinetic stability of aqueous dispersions quantitatively and describes the force between charged surfaces interacting through a liquid medium. It combines the effects of the van der Waals attraction and the electrostatic repulsion due to the so-called double layer of counterions. The electrostatic part of the DLVO interaction is computed in the mean field approximation in the limit of low surface potentials - that is when the potential energy of an elementary charge on the surface is much smaller than the thermal energy scale, . For two spheres of radius each having a charge separated by a center-to-center distance in a fluid of dielectric constant containing a concentration of monovalent ions, the electrostatic potential takes the form of a screened-Coulomb or Yukawa potential,

Polyelectrolytes are polymers whose repeating units bear an electrolyte group. Polycations and polyanions are polyelectrolytes. These groups dissociate in aqueous solutions (water), making the polymers charged. Polyelectrolyte properties are thus similar to both electrolytes (salts) and polymers and are sometimes called polysalts. Like salts, their solutions are electrically conductive. Like polymers, their solutions are often viscous. Charged molecular chains, commonly present in soft matter systems, play a fundamental role in determining structure, stability and the interactions of various molecular assemblies. Theoretical approaches to describing their statistical properties differ profoundly from those of their electrically neutral counterparts, while technological and industrial fields exploit their unique properties. Many biological molecules are polyelectrolytes. For instance, polypeptides, glycosaminoglycans, and DNA are polyelectrolytes. Both natural and synthetic polyelectrolytes are used in a variety of industries.
Electrical mobility is the ability of charged particles to move through a medium in response to an electric field that is pulling them. The separation of ions according to their mobility in gas phase is called ion mobility spectrometry, in liquid phase it is called electrophoresis.
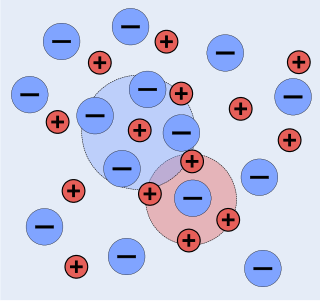
The chemists Peter Debye and Erich Hückel noticed that solutions that contain ionic solutes do not behave ideally even at very low concentrations. So, while the concentration of the solutes is fundamental to the calculation of the dynamics of a solution, they theorized that an extra factor that they termed gamma is necessary to the calculation of the activities of the solution. Hence they developed the Debye–Hückel equation and Debye–Hückel limiting law. The activity is only proportional to the concentration and is altered by a factor known as the activity coefficient . This factor takes into account the interaction energy of ions in solution.
A surface charge is an electric charge present on a two-dimensional surface. These electric charges are constrained on this 2-D surface, and surface charge density, measured in coulombs per square meter (C•m−2), is used to describe the charge distribution on the surface. The electric potential is continuous across a surface charge and the electric field is discontinuous, but not infinite; this is unless the surface charge consists of a dipole layer. In comparison, the potential and electric field both diverge at any point charge or linear charge.
In physics, Larmor precession is the precession of the magnetic moment of an object about an external magnetic field. The phenomenon is conceptually similar to the precession of a tilted classical gyroscope in an external torque-exerting gravitational field. Objects with a magnetic moment also have angular momentum and effective internal electric current proportional to their angular momentum; these include electrons, protons, other fermions, many atomic and nuclear systems, as well as classical macroscopic systems. The external magnetic field exerts a torque on the magnetic moment,

The mass-to-charge ratio (m/Q) is a physical quantity relating the mass (quantity of matter) and the electric charge of a given particle, expressed in units of kilograms per coulomb (kg/C). It is most widely used in the electrodynamics of charged particles, e.g. in electron optics and ion optics.
The plasma parameter is a dimensionless number, denoted by capital Lambda, Λ. The plasma parameter is usually interpreted to be the argument of the Coulomb logarithm, which is the ratio of the maximum impact parameter to the classical distance of closest approach in Coulomb scattering. In this case, the plasma parameter is given by:
The Poisson–Boltzmann equation is a useful equation in many settings, whether it be to understand physiological interfaces, polymer science, electron interactions in a semiconductor, or more. It aims to describe the distribution of the electric potential in solution in the direction normal to a charged surface. This distribution is important to determine how the electrostatic interactions will affect the molecules in solution. The Poisson–Boltzmann equation is derived via mean-field assumptions. From the Poisson–Boltzmann equation many other equations have been derived with a number of different assumptions.
The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes and plasmas. It is a linearized Poisson–Boltzmann model, which assumes an extremely simplified model of electrolyte solution but nevertheless gave accurate predictions of mean activity coefficients for ions in dilute solution. The Debye–Hückel equation provides a starting point for modern treatments of non-ideality of electrolyte solutions.
The molar conductivity of an electrolyte solution is defined as its conductivity divided by its molar concentration.

Conductivity of an electrolyte solution is a measure of its ability to conduct electricity. The SI unit of conductivity is Siemens per meter (S/m).
Pitzer equations are important for the understanding of the behaviour of ions dissolved in natural waters such as rivers, lakes and sea-water. They were first described by physical chemist Kenneth Pitzer. The parameters of the Pitzer equations are linear combinations of parameters, of a virial expansion of the excess Gibbs free energy, which characterise interactions amongst ions and solvent. The derivation is thermodynamically rigorous at a given level of expansion. The parameters may be derived from various experimental data such as the osmotic coefficient, mixed ion activity coefficients, and salt solubility. They can be used to calculate mixed ion activity coefficients and water activities in solutions of high ionic strength for which the Debye–Hückel theory is no longer adequate. They are more rigorous than the equations of specific ion interaction theory, but Pitzer parameters are more difficult to determine experimentally than SIT parameters.
Adsorption of polyelectrolytes on solid substrates is a surface phenomenon where long-chained polymer molecules with charged groups bind to a surface that is charged in the opposite polarity. On the molecular level, the polymers do not actually bond to the surface, but tend to "stick" to the surface via intermolecular forces and the charges created by the dissociation of various side groups of the polymer. Because the polymer molecules are so long, they have a large amount of surface area with which to contact the surface and thus do not desorb as small molecules are likely to do. This means that adsorbed layers of polyelectrolytes form a very durable coating. Due to this important characteristic of polyelectrolyte layers they are used extensively in industry as flocculants, for solubilization, as supersorbers, antistatic agents, as oil recovery aids, as gelling aids in nutrition, additives in concrete, or for blood compatibility enhancement to name a few.
In chemistry, ion transport number, also called the transference number, is the fraction of the total electric current carried in an electrolyte by a given ionic species i:
Polyelectrolytes are charged polymers capable of stabilizing colloidal emulsions through electrostatic interactions. Their effectiveness can be dependent on molecular weight, pH, solvent polarity, ionic strength, and the hydrophilic-lipophilic balance (HLB). Stabilized emulsions are useful in many industrial processes, including deflocculation, drug delivery, petroleum waste treatment, and food technology.
Adiabatic electron-transfer is a type of oxidation-reduction processes. The mechanism is ubiquitous in nature in both the inorganic and biological spheres. Adiabatic electron-transfers proceed without making or breaking chemical bonds. Adiabatic electron-transfer can occur by either optical or thermal mechanisms. Electron transfer during a collision between an oxidant and a reductant occurs adiabatically on a continuous potential-energy surface.










