Coupled mode theory

Last updated

Coupled mode theory (CMT) is a perturbational approach for analyzing the coupling of vibrational systems (mechanical, optical, electrical, etc.) in space or in time. Coupled mode theory allows a wide range of devices and systems to be modeled as one or more coupled resonators. In optics, such systems include laser cavities, photonic crystal slabs, metamaterials, and ring resonators.

Contents

History

Coupled mode theory first arose in the 1950s in the works of Miller on microwave transmission lines, [1] Pierce on electron beams, [2] and Gould on backward wave oscillators. [3] This put in place the mathematical foundations for the modern formulation expressed by H. A. Haus et al. for optical waveguides. [4] [5]

In the late 1990s and early 2000s, the field of nanophotonics has revitalized interest in coupled mode theory. Coupled mode theory has been used to account for the Fano resonances in photonic crystal slabs [6] and has also been modified to account for optical resonators with non-orthogonal modes. [7] Since late 2000s, researchers have capitalized on coupled mode theory to explain the concept of magnetically coupled resonators. [8] [9]

Overview

The oscillatory systems to which coupled mode theory applies are described by second order partial differential equations. CMT allows the second order partial differential equation to be expressed as one or more coupled first order ordinary differential equations. The following assumptions are generally made with CMT:

Formulation

The formulation of the coupled mode theory is based on the development of the solution to an electromagnetic problem into modes. Most of the time it is eigenmodes which are taken in order to form a complete base. The choice of the basis and the adoption of certain hypothesis like parabolic approximation differs from formulation to formulation. The classification proposed by [10] of the different formulation is as follows:

  1. The choice of starting differential equation. some of the coupled mode theories are derived directly from the Maxwell differential equations [11] [12] although others use simplifications in order to obtain a Helmholtz equation.
  2. The choice of principle to derive the equations of the CMT. Either the reciprocity theorem [11] [12] or the variational principle have been used.
  3. The choice of orthogonality product used to establish the eigenmode base. Some references use the unconjugated form [11] and others the complex-conjugated form. [12]
  4. Finally, the choice of the form of the equation, either vectorial [11] [12] or scalar.

When n modes of an electromagnetic wave propagate through a media in the direction z without loss, the power transported by each mode is described by a modal power Pm. At a given frequency ω.

where Nm is the norm of the mth mode and am is the modal amplitude.

See also

Related Research Articles

<span class="mw-page-title-main">Circulator</span> Electronic circuit in which a signal entering any port exits at the next port

In electrical engineering, a circulator is a passive, non-reciprocal three- or four-port device that only allows a microwave or radio-frequency (RF) signal to exit through the port directly after the one it entered. Optical circulators have similar behavior. Ports are where an external waveguide or transmission line, such as a microstrip line or a coaxial cable, connects to the device. For a three-port circulator, a signal applied to port 1 only comes out of port 2; a signal applied to port 2 only comes out of port 3; a signal applied to port 3 only comes out of port 1. An ideal three-port circulator thus has the following scattering matrix:

<span class="mw-page-title-main">Cutoff frequency</span> Frequency response boundary

In physics and electrical engineering, a cutoff frequency, corner frequency, or break frequency is a boundary in a system's frequency response at which energy flowing through the system begins to be reduced rather than passing through.

<span class="mw-page-title-main">Transmission line</span> Cable or other structure for carrying radio waves

In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmission must be taken into account. This applies especially to radio-frequency engineering because the short wavelengths mean that wave phenomena arise over very short distances. However, the theory of transmission lines was historically developed to explain phenomena on very long telegraph lines, especially submarine telegraph cables.

<span class="mw-page-title-main">Waveguide</span> Structure that guides waves efficiently

A waveguide is a structure that guides waves by restricting the transmission of energy to one direction. Common types of waveguides include acoustic waveguides which direct sound, optical waveguides which direct light, and radio-frequency waveguides which direct electromagnetic waves other than light like radio waves.

In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source. Even when there is a propagating electromagnetic wave produced, one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths.

Quasinormal modes (QNM) are the modes of energy dissipation of a perturbed object or field, i.e. they describe perturbations of a field that decay in time.

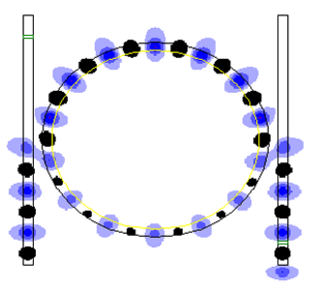
<span class="mw-page-title-main">Optical ring resonators</span>

An optical ring resonator is a set of waveguides in which at least one is a closed loop coupled to some sort of light input and output. The concepts behind optical ring resonators are the same as those behind whispering galleries except that they use light and obey the properties behind constructive interference and total internal reflection. When light of the resonant wavelength is passed through the loop from the input waveguide, the light builds up in intensity over multiple round-trips owing to constructive interference and is output to the output bus waveguide which serves as a detector waveguide. Because only a select few wavelengths will be at resonance within the loop, the optical ring resonator functions as a filter. Additionally, as implied earlier, two or more ring waveguides can be coupled to each other to form an add/drop optical filter.

<span class="mw-page-title-main">Computational electromagnetics</span> Branch of physics

Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers.

The finite-difference frequency-domain (FDFD) method is a numerical solution method for problems usually in electromagnetism and sometimes in acoustics, based on finite-difference approximations of the derivative operators in the differential equation being solved.

Characteristic modes (CM) form a set of functions which, under specific boundary conditions, diagonalizes operator relating field and induced sources. Under certain conditions, the set of the CM is unique and complete (at least theoretically) and thereby capable of describing the behavior of a studied object in full.

Eigenmode expansion (EME) is a computational electrodynamics modelling technique. It is also referred to as the mode matching technique or the bidirectional eigenmode propagation method. Eigenmode expansion is a linear frequency-domain method.

In mathematics and electronics, Cavity perturbation theory describes methods for derivation of perturbation formulae for performance changes of a cavity resonator.

Circuit quantum electrodynamics provides a means of studying the fundamental interaction between light and matter. As in the field of cavity quantum electrodynamics, a single photon within a single mode cavity coherently couples to a quantum object (atom). In contrast to cavity QED, the photon is stored in a one-dimensional on-chip resonator and the quantum object is no natural atom but an artificial one. These artificial atoms usually are mesoscopic devices which exhibit an atom-like energy spectrum. The field of circuit QED is a prominent example for quantum information processing and a promising candidate for future quantum computation.

<span class="mw-page-title-main">Semiconductor laser theory</span> Theory of laser diodes

Semiconductor lasers or laser diodes play an important part in our everyday lives by providing cheap and compact-size lasers. They consist of complex multi-layer structures requiring nanometer scale accuracy and an elaborate design. Their theoretical description is important not only from a fundamental point of view, but also in order to generate new and improved designs. It is common to all systems that the laser is an inverted carrier density system. The carrier inversion results in an electromagnetic polarization which drives an electric field . In most cases, the electric field is confined in a resonator, the properties of which are also important factors for laser performance.

<span class="mw-page-title-main">Coplanar waveguide</span> Type of planar transmission line

Coplanar waveguide is a type of electrical planar transmission line which can be fabricated using printed circuit board technology, and is used to convey microwave-frequency signals. On a smaller scale, coplanar waveguide transmission lines are also built into monolithic microwave integrated circuits.

<span class="mw-page-title-main">Frequency selective surface</span> Optical filter

A frequency-selective surface (FSS) is any thin, repetitive surface designed to reflect, transmit or absorb electromagnetic fields based on the frequency of the field. In this sense, an FSS is a type of optical filter or metal-mesh optical filters in which the filtering is accomplished by virtue of the regular, periodic pattern on the surface of the FSS. Though not explicitly mentioned in the name, FSS's also have properties which vary with incidence angle and polarization as well - these are unavoidable consequences of the way in which FSS's are constructed. Frequency-selective surfaces have been most commonly used in the radio frequency region of the electromagnetic spectrum and find use in applications as diverse as the aforementioned microwave oven, antenna radomes and modern metamaterials. Sometimes frequency selective surfaces are referred to simply as periodic surfaces and are a 2-dimensional analog of the new periodic volumes known as photonic crystals.

<span class="mw-page-title-main">Cavity optomechanics</span>

Cavity optomechanics is a branch of physics which focuses on the interaction between light and mechanical objects on low-energy scales. It is a cross field of optics, quantum optics, solid-state physics and materials science. The motivation for research on cavity optomechanics comes from fundamental effects of quantum theory and gravity, as well as technological applications.

<span class="mw-page-title-main">Loop-gap resonator</span>

A loop-gap resonator (LGR) is an electromagnetic resonator that operates in the radio and microwave frequency ranges. The simplest LGRs are made from a conducting tube with a narrow slit cut along its length. The LGR dimensions are typically much smaller than the free-space wavelength of the electromagnetic fields at the resonant frequency. Therefore, relatively compact LGRs can be designed to operate at frequencies that are too low to be accessed using, for example, cavity resonators. These structures can have very sharp resonances making them useful for electron spin resonance (ESR) experiments, and precision measurements of electromagnetic material properties.

In nonlinear systems, a resonant interaction is the interaction of three or more waves, usually but not always of small amplitude. Resonant interactions occur when a simple set of criteria coupling wave-vectors and the dispersion equation are met. The simplicity of the criteria make technique popular in multiple fields. Its most prominent and well-developed forms appear in the study of gravity waves, but also finds numerous applications from astrophysics and biology to engineering and medicine. Theoretical work on partial differential equations provides insights into chaos theory; there are curious links to number theory. Resonant interactions allow waves to (elastically) scatter, diffuse or to become unstable. Diffusion processes are responsible for the eventual thermalization of most nonlinear systems; instabilities offer insight into high-dimensional chaos and turbulence.

<span class="mw-page-title-main">Method of moments (electromagnetics)</span> Numerical method in computational electromagnetics

The method of moments (MoM), also known as the moment method and method of weighted residuals, is a numerical method in computational electromagnetics. It is used in computer programs that simulate the interaction of electromagnetic fields such as radio waves with matter, for example antenna simulation programs like NEC that calculate the radiation pattern of an antenna. Generally being a frequency-domain method, it involves the projection of an integral equation into a system of linear equations by the application of appropriate boundary conditions. This is done by using discrete meshes as in finite difference and finite element methods, often for the surface. The solutions are represented with the linear combination of pre-defined basis functions; generally, the coefficients of these basis functions are the sought unknowns. Green's functions and Galerkin method play a central role in the method of moments.

References

  1. ↑ S.E.Miller,"Coupled wave theory and waveguide applications.", Bell System Technical Journal, 1954
  2. ↑ J. R. Pierce, "Coupling of modes of propagations", Journal of Applied Physics, 25, 1954
  3. ↑ R.W. Gould, "A coupled mode description of the backward-wave oscillator and the Kompfner dip condition" I.R.E. Trans. Electron Devices, vol. PGED-2, pp. 37–42, 1955.
  4. ↑ Haus, H., et al. "Coupled-mode theory of optical waveguides." Journal of Lightwave Technology 5.1 (1987): 16-23.
  5. ↑ H. A. Haus, W. P. Huang. "Coupled Mode Theory."Proceedings of the IEEE, Vol 19, No 10, October 1991.
  6. ↑ S. Fan, W. Suh, J. Joannopoulos, "Temporal coupled-mode theory for the Fano resonance in optical resonators," JOSA A, vol. 20, no. 3, pp. 569–572, 2003.
  7. ↑ W. Suh, Z. Wang, and S. Fan, "Temporal coupled-mode theory and the presence of non-orthogonal modes in lossless multimode cavities," Quantum Electronics, IEEE Journal of, vol. 40, no. 10, pp. 1511–1518, 2004
  8. ↑ Elnaggar S.Y., Tervo, R.J., and Mattar, S.M., Energy Coupled Mode Theory for Electromagnetic Resonators, IEEE Transactions on Microwave Theory and Techniques, vol. 63, no. 7, pp. 2115-2123, July 2015, doi: 10.1109/TMTT.2015.2434377.
  9. ↑ Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J. D.; Fisher, P.; Soljacic, M. (6 July 2007). "Wireless Power Transfer via Strongly Coupled Magnetic Resonances". Science. 317 (5834): 83–86. Bibcode:2007Sci...317...83K. CiteSeerX   10.1.1.418.9645 . doi:10.1126/science.1143254. PMID   17556549. S2CID   17105396.
  10. ↑ Barybin and Dmitriev,"Modern Electrodynamics and Coupled-mode theory", 2002
  11. 1 2 3 4 Hardy and Streifer, "Coupled mode theory of parallel waveguides", Journal of Lightwave Technology,1985
  12. 1 2 3 4 A. W. Snyder and J. D. Love, "Optical waveguide Theory", Chapman and Hall, 1983
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.