
In physics and materials science, plasticity is the ability of a solid material to undergo permanent deformation, a non-reversible change of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the material itself. In engineering, the transition from elastic behavior to plastic behavior is known as yielding.
The field of strength of materials typically refers to various methods of calculating the stresses and strains in structural members, such as beams, columns, and shafts. The methods employed to predict the response of a structure under loading and its susceptibility to various failure modes takes into account the properties of the materials such as its yield strength, ultimate strength, Young's modulus, and Poisson's ratio. In addition, the mechanical element's macroscopic properties such as its length, width, thickness, boundary constraints and abrupt changes in geometry such as holes are considered.

In materials science, fatigue is the initiation and propagation of cracks in a material due to cyclic loading. Once a fatigue crack has initiated, it grows a small amount with each loading cycle, typically producing striations on some parts of the fracture surface. The crack will continue to grow until it reaches a critical size, which occurs when the stress intensity factor of the crack exceeds the fracture toughness of the material, producing rapid propagation and typically complete fracture of the structure.
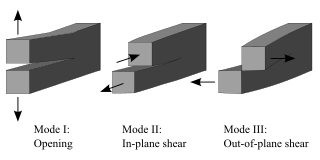
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.

The rainflow-counting algorithm is used in calculating the fatigue life of a component in order to convert a uniaxial loading sequence of varying stress into an equivalent set of constant amplitude stress reversals. The method successively extracts the smaller interruption cycles from a sequence, which models the material memory effect seen with stress-strain hysteresis cycles. This simplification allows the number of cycles until failure of a component to be determined for each rainflow cycle using either Miner's rule to calculate the fatigue damage, or in a crack growth equation to calculate the crack increments. Both methods give an estimate of the fatigue life of a component. In cases of multiaxial loading, critical plane analysis can be used together with rainflow counting to identify the uniaxial history associated with the plane that maximizes damage. The algorithm was developed by Tatsuo Endo and M. Matsuishi in 1968.
In safe-life design, products are intended to be removed from service at a specific design life.
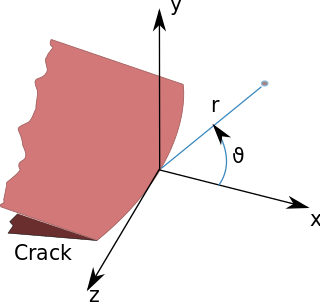
In fracture mechanics, the stress intensity factor is used to predict the stress state near the tip of a crack or notch caused by a remote load or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic material and is useful for providing a failure criterion for brittle materials, and is a critical technique in the discipline of damage tolerance. The concept can also be applied to materials that exhibit small-scale yielding at a crack tip.
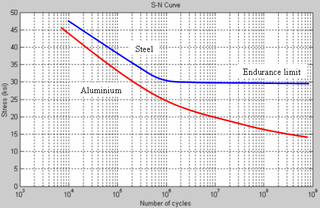
The fatigue limit or endurance limit is the stress level below which an infinite number of loading cycles can be applied to a material without causing fatigue failure. Some metals such as ferrous alloys and titanium alloys have a distinct limit, whereas others such as aluminium and copper do not and will eventually fail even from small stress amplitudes. Where materials do not have a distinct limit the term fatigue strength or endurance strength is used and is defined as the maximum value of completely reversed bending stress that a material can withstand for a specified number of cycles without a fatigue failure.
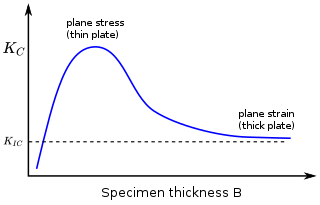
In materials science, fracture toughness is the critical stress intensity factor of a sharp crack where propagation of the crack suddenly becomes rapid and unlimited. A component's thickness affects the constraint conditions at the tip of a crack with thin components having plane stress conditions and thick components having plane strain conditions. Plane strain conditions give the lowest fracture toughness value which is a material property. The critical value of stress intensity factor in mode I loading measured under plane strain conditions is known as the plane strain fracture toughness, denoted . When a test fails to meet the thickness and other test requirements that are in place to ensure plane strain conditions, the fracture toughness value produced is given the designation . Fracture toughness is a quantitative way of expressing a material's resistance to crack propagation and standard values for a given material are generally available.

Fractography is the study of the fracture surfaces of materials. Fractographic methods are routinely used to determine the cause of failure in engineering structures, especially in product failure and the practice of forensic engineering or failure analysis. In material science research, fractography is used to develop and evaluate theoretical models of crack growth behavior.
AFGROW is a Damage Tolerance Analysis (DTA) computer program that calculates crack initiation, fatigue crack growth, and fracture to predict the life of metallic structures. Originally developed by the Air Force Research Laboratory, AFGROW is mainly used for aerospace applications, but can be applied to any type of metallic structure that experiences fatigue cracking.
Material failure theory is an interdisciplinary field of materials science and solid mechanics which attempts to predict the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure (fracture) or ductile failure (yield). Depending on the conditions most materials can fail in a brittle or ductile manner or both. However, for most practical situations, a material may be classified as either brittle or ductile.
Polymer fracture is the study of the fracture surface of an already failed material to determine the method of crack formation and extension in polymers both fiber reinforced and otherwise. Failure in polymer components can occur at relatively low stress levels, far below the tensile strength because of four major reasons: long term stress or creep rupture, cyclic stresses or fatigue, the presence of structural flaws and stress-cracking agents. Formations of submicroscopic cracks in polymers under load have been studied by x ray scattering techniques and the main regularities of crack formation under different loading conditions have been analyzed. The low strength of polymers compared to theoretically predicted values are mainly due to the many microscopic imperfections found in the material. These defects namely dislocations, crystalline boundaries, amorphous interlayers and block structure can all lead to the non-uniform distribution of mechanical stress.
Crack closure is a phenomenon in fatigue loading, where the opposing faces of a crack remain in contact even with an external load acting on the material. As the load is increased, a critical value will be reached at which time the crack becomes open. Crack closure occurs from the presence of material propping open the crack faces and can arise from many sources including plastic deformation or phase transformation during crack propagation, corrosion of crack surfaces, presence of fluids in the crack, or roughness at cracked surfaces.
Engineering Critical Assessment (ECA) is a procedure by which the safety of a welded structure with defects or flaws can be determined. ECAs utilize the material properties and expected stress history to determine a flaw acceptance criteria which will ensure that welds will not fail during the construction or service life of the welded structure. The assessment can be used before the structure is in use, or during in-service inspection, to determine whether a given weld is in need of repair. ECAs are used throughout the energy, manufacturing, and infrastructure industries. ECAs are based heavily upon fracture mechanics principles, and reflect an improvement over traditional methods of weld quality assurance, which can be arbitrary or overly conservative.
In continuum mechanics, ratcheting, or ratchetting, also known as cyclic creep, is a behavior in which plastic deformation accumulates due to cyclic mechanical or thermal stress.

Striations are marks produced on the fracture surface that show the incremental growth of a fatigue crack. A striation marks the position of the crack tip at the time it was made. The term striation generally refers to ductile striations which are rounded bands on the fracture surface separated by depressions or fissures and can have the same appearance on both sides of the mating surfaces of the fatigue crack. Although some research has suggested that many loading cycles are required to form a single striation, it is now generally thought that each striation is the result of a single loading cycle.

A crack growth equation is used for calculating the size of a fatigue crack growing from cyclic loads. The growth of fatigue cracks can result in catastrophic failure, particularly in the case of aircraft. A crack growth equation can be used to ensure safety, both in the design phase and during operation, by predicting the size of cracks. In critical structure, loads can be recorded and used to predict the size of cracks to ensure maintenance or retirement occurs prior to any of the cracks failing.

Slip bands or stretcher-strain marks are localized bands of plastic deformation in metals experiencing stresses. Formation of slip bands indicates a concentrated unidirectional slip on certain planes causing a stress concentration. Typically, slip bands induce surface steps and a stress concentration which can be a crack nucleation site. Slip bands extend until impinged by a boundary, and the generated stress from dislocations pile-up against that boundary will either stop or transmit the operating slip depening on its (mis)orientation.











