
In linear algebra, the singular value decomposition (SVD) is a factorization of a real or complex matrix into a rotation, followed by a rescaling followed by another rotation. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any matrix. It is related to the polar decomposition.
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant. For instance, the following matrix is a Toeplitz matrix:
In mathematics, a Hermitian matrix is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the i-th row and j-th column is equal to the complex conjugate of the element in the j-th row and i-th column, for all indices i and j:
In the mathematical discipline of linear algebra, a matrix decomposition or matrix factorization is a factorization of a matrix into a product of matrices. There are many different matrix decompositions; each finds use among a particular class of problems.
In numerical analysis, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.
In linear algebra, a tridiagonal matrix is a band matrix that has nonzero elements only on the main diagonal, the subdiagonal/lower diagonal, and the supradiagonal/upper diagonal. For example, the following matrix is tridiagonal:
In matrix theory, the Perron–Frobenius theorem, proved by Oskar Perron (1907) and Georg Frobenius (1912), asserts that a real square matrix with positive entries has a unique eigenvalue of largest magnitude and that eigenvalue is real. The corresponding eigenvector can be chosen to have strictly positive components, and also asserts a similar statement for certain classes of nonnegative matrices. This theorem has important applications to probability theory ; to the theory of dynamical systems ; to economics ; to demography ; to social networks ; to Internet search engines (PageRank); and even to ranking of American football teams. The first to discuss the ordering of players within tournaments using Perron–Frobenius eigenvectors is Edmund Landau.
In mathematics, we can define norms for the elements of a vector space. When the vector space in question consists of matrices, these are called matrix norms.
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable—that is, a matrix in which some or all elements are random variables. Many important properties of physical systems can be represented mathematically as matrix problems. For example, the thermal conductivity of a lattice can be computed from the dynamical matrix of the particle-particle interactions within the lattice.
Simple rational approximation (SRA) is a subset of interpolating methods using rational functions. Especially, SRA interpolates a given function with a specific rational function whose poles and zeros are simple, which means that there is no multiplicity in poles and zeros. Sometimes, it only implies simple poles.
In functional analysis, the dual norm is a measure of size for a continuous linear function defined on a normed vector space.
In mathematics, the logarithmic norm is a real-valued functional on operators, and is derived from either an inner product, a vector norm, or its induced operator norm. The logarithmic norm was independently introduced by Germund Dahlquist and Sergei Lozinskiĭ in 1958, for square matrices. It has since been extended to nonlinear operators and unbounded operators as well. The logarithmic norm has a wide range of applications, in particular in matrix theory, differential equations and numerical analysis. In the finite-dimensional setting, it is also referred to as the matrix measure or the Lozinskiĭ measure.
In numerical linear algebra, the alternating-direction implicit (ADI) method is an iterative method used to solve Sylvester matrix equations. It is a popular method for solving the large matrix equations that arise in systems theory and control, and can be formulated to construct solutions in a memory-efficient, factored form. It is also used to numerically solve parabolic and elliptic partial differential equations, and is a classic method used for modeling heat conduction and solving the diffusion equation in two or more dimensions. It is an example of an operator splitting method.
In the mathematical field of linear algebra and convex analysis, the numerical range or field of values of a complex matrix A is the set
In theoretical computer science, the computational complexity of matrix multiplication dictates how quickly the operation of matrix multiplication can be performed. Matrix multiplication algorithms are a central subroutine in theoretical and numerical algorithms for numerical linear algebra and optimization, so finding the fastest algorithm for matrix multiplication is of major practical relevance.
A Jacobi operator, also known as Jacobi matrix, is a symmetric linear operator acting on sequences which is given by an infinite tridiagonal matrix. It is commonly used to specify systems of orthonormal polynomials over a finite, positive Borel measure. This operator is named after Carl Gustav Jacob Jacobi.
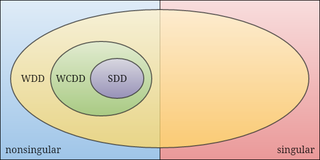
In mathematics, the weakly chained diagonally dominant matrices are a family of nonsingular matrices that include the strictly diagonally dominant matrices.
In statistics, the complex Wishart distribution is a complex version of the Wishart distribution. It is the distribution of times the sample Hermitian covariance matrix of zero-mean independent Gaussian random variables. It has support for Hermitian positive definite matrices.
Beresford Neill Parlett is an English applied mathematician, specializing in numerical analysis and scientific computation.
In matrix analysis, Kreiss matrix theorem relates the so-called Kreiss constant of a matrix with the power iterates of this matrix. It was originally introduced by Heinz-Otto Kreiss to analyze the stability of finite difference methods for partial difference equations.












