DPLL(T)

Last updated

In computer science, DPLL(T) is a framework for determining the satisfiability of SMT problems. The algorithm extends the original SAT-solving DPLL algorithm with the ability to reason about an arbitrary theory T. [1] [2] [3] At a high level, the algorithm works by transforming an SMT problem into a SAT formula where atoms are replaced with Boolean variables. The algorithm repeatedly finds a satisfying valuation for the SAT problem, consults a theory solver to check consistency under the domain-specific theory, and then (if a contradiction is found) refines the SAT formula with this information. [4]

Many modern SMT solvers, such as Microsoft's Z3 Theorem Prover and CVC4, use DPLL(T) to power their core solving capabilities. [5] [6] [7]

Related Research Articles

Automated theorem proving is a subfield of automated reasoning and mathematical logic dealing with proving mathematical theorems by computer programs. Automated reasoning over mathematical proof was a major motivating factor for the development of computer science.

In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.

In computer science, formal methods are mathematically rigorous techniques for the specification, development, analysis, and verification of software and hardware systems. The use of formal methods for software and hardware design is motivated by the expectation that, as in other engineering disciplines, performing appropriate mathematical analysis can contribute to the reliability and robustness of a design.

<span class="mw-page-title-main">Martin Davis (mathematician)</span> American mathematician (1928–2023)

Martin David Davis was an American mathematician and computer scientist who contributed to the fields of computability theory and mathematical logic. His work on Hilbert's tenth problem led to the MRDP theorem. He also advanced the Post–Turing model and co-developed the Davis–Putnam–Logemann–Loveland (DPLL) algorithm, which is foundational for Boolean satisfiability solvers.

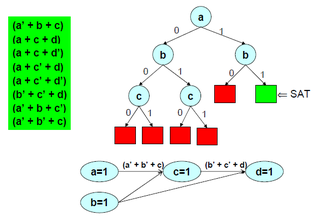
<span class="mw-page-title-main">DPLL algorithm</span> Type of search algorithm

In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem.

In computational complexity theory, the maximum satisfiability problem (MAX-SAT) is the problem of determining the maximum number of clauses, of a given Boolean formula in conjunctive normal form, that can be made true by an assignment of truth values to the variables of the formula. It is a generalization of the Boolean satisfiability problem, which asks whether there exists a truth assignment that makes all clauses true.

In computer science and mathematical logic, satisfiability modulo theories (SMT) is the problem of determining whether a mathematical formula is satisfiable. It generalizes the Boolean satisfiability problem (SAT) to more complex formulas involving real numbers, integers, and/or various data structures such as lists, arrays, bit vectors, and strings. The name is derived from the fact that these expressions are interpreted within ("modulo") a certain formal theory in first-order logic with equality. SMT solvers are tools that aim to solve the SMT problem for a practical subset of inputs. SMT solvers such as Z3 and cvc5 have been used as a building block for a wide range of applications across computer science, including in automated theorem proving, program analysis, program verification, and software testing.

The Bernays–Schönfinkel class of formulas, named after Paul Bernays, Moses Schönfinkel and Frank P. Ramsey, is a fragment of first-order logic formulas where satisfiability is decidable.

In mathematical logic, monadic second-order logic (MSO) is the fragment of second-order logic where the second-order quantification is limited to quantification over sets. It is particularly important in the logic of graphs, because of Courcelle's theorem, which provides algorithms for evaluating monadic second-order formulas over graphs of bounded treewidth. It is also of fundamental importance in automata theory, where the Büchi–Elgot–Trakhtenbrot theorem gives a logical characterization of the regular languages.

In computer science and formal methods, a SAT solver is a computer program which aims to solve the Boolean satisfiability problem. On input a formula over Boolean variables, such as "(x or y) and (x or not y)", a SAT solver outputs whether the formula is satisfiable, meaning that there are possible values of x and y which make the formula true, or unsatisfiable, meaning that there are no such values of x and y. In this case, the formula is satisfiable when x is true, so the solver should return "satisfiable". Since the introduction of algorithms for SAT in the 1960s, modern SAT solvers have grown into complex software artifacts involving a large number of heuristics and program optimizations to work efficiently.

The CADE ATP System Competition (CASC) is an annual competition of fully automated theorem provers for classical logic

In mathematical logic, an uninterpreted function or function symbol is one that has no other property than its name and n-ary form. Function symbols are used, together with constants and variables, to form terms.

In computer science, conflict-driven clause learning (CDCL) is an algorithm for solving the Boolean satisfiability problem (SAT). Given a Boolean formula, the SAT problem asks for an assignment of variables so that the entire formula evaluates to true. The internal workings of CDCL SAT solvers were inspired by DPLL solvers. The main difference between CDCL and DPLL is that CDCL's backjumping is non-chronological.

David Lansing Dill is a computer scientist and academic noted for contributions to formal verification, electronic voting security, and computational systems biology.

Z3, also known as the Z3 Theorem Prover, is a satisfiability modulo theories (SMT) solver developed by Microsoft.

In computer science, an e-graph is a data structure that stores an equivalence relation over terms of some language.

<span class="mw-page-title-main">Ofer Strichman</span>

Ofer Strichman is a professor of computational logic and computer science at the Davidson Industrial Engineering and Management, Technion – Israel Institute of Technology. He holds the Joseph Gruenblat chair in production engineering.

In computer science and mathematical logic, Cooperating Validity Checker (CVC) is a family of satisfiability modulo theories (SMT) solvers. The latest major versions of CVC are CVC4 and CVC5 ; earlier versions include CVC, CVC Lite, and CVC3. Both CVC4 and cvc5 support the SMT-LIB and TPTP input formats for solving SMT problems, and the SyGuS-IF format for program synthesis. Both CVC4 and cvc5 can output proofs that can be independently checked in the LFSC format, cvc5 additionally supports the Alethe and Lean 4 formats. cvc5 has bindings for C++, Python, and Java.

Constrained Horn clauses (CHCs) are a fragment of first-order logic with applications to program verification and synthesis. Constrained Horn clauses can be seen as a form of constraint logic programming.

Counterexample-guided abstraction refinement (CEGAR) is a technique for symbolic model checking. It is also applied in modal logic tableau calculi algorithms to optimise their efficiency.

References

  1. ↑ Ganzinger, Harald; Hagen, George; Nieuwenhuis, Robert; Oliveras, Albert; Tinelli, Cesare (2004). "DPLL(T): Fast Decision Procedures". In Alur, Rajeev; Peled, Doron A. (eds.). Computer Aided Verification. Lecture Notes in Computer Science. Vol. 3114. Springer Berlin Heidelberg. pp. 175–188. doi: 10.1007/978-3-540-27813-9_14 . ISBN   9783540278139.
  2. ↑ Nieuwenhuis, Robert; Oliveras, Albert; Tinelli, Cesare (2006). "Solving SAT and SAT Modulo Theories: From an Abstract Davis–Putnam–Logemann–Loveland Procedure to DPLL(T)". J. ACM. 53 (6): 937–977. doi:10.1145/1217856.1217859. ISSN   0004-5411. S2CID   14058631.
  3. ↑ Nieuwenhuis, Robert; Oliveras, Albert (2005). "DPLL(T) with Exhaustive Theory Propagation and Its Application to Difference Logic". In Etessami, Kousha; Rajamani, Sriram K. (eds.). Computer Aided Verification. Lecture Notes in Computer Science. Vol. 3576. Springer Berlin Heidelberg. pp. 321–334. doi: 10.1007/11513988_33 . ISBN   9783540316862.
  4. ↑ Reynolds, Andrew (2015). "Satisfiability Modulo Theories and DPLL(T)" (PDF). The University of Iowa. Retrieved 2019-04-08.
  5. ↑ de Moura, Leonardo; Bjørner, Nikolaj (2008). "Z3: An Efficient SMT Solver". In Ramakrishnan, C. R.; Rehof, Jakob (eds.). Tools and Algorithms for the Construction and Analysis of Systems. Lecture Notes in Computer Science. Vol. 4963. Springer Berlin Heidelberg. pp. 337–340. doi: 10.1007/978-3-540-78800-3_24 . ISBN   9783540788003.
  6. ↑ Liang, Tianyi; Reynolds, Andrew; Tinelli, Cesare; Barrett, Clark; Deters, Morgan (2014). "A DPLL(T) Theory Solver for a Theory of Strings and Regular Expressions". In Biere, Armin; Bloem, Roderick (eds.). Computer Aided Verification. Lecture Notes in Computer Science. Cham: Springer International Publishing. pp. 646–662. doi: 10.1007/978-3-319-08867-9_43 . ISBN   978-3-319-08867-9.
  7. ↑ Bruttomesso, Roberto; Cimatti, Alessandro; Franzén, Anders; Griggio, Alberto; Sebastiani, Roberto (2008). "The MathSAT 4 SMT Solver". In Gupta, Aarti; Malik, Sharad (eds.). Computer Aided Verification. Lecture Notes in Computer Science. Vol. 5123. Springer Berlin Heidelberg. pp. 299–303. doi: 10.1007/978-3-540-70545-1_28 . ISBN   9783540705451.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.