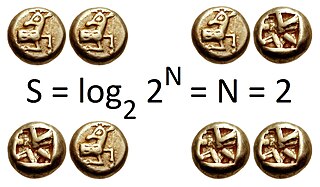In algorithmic information theory, the Kolmogorov complexity of an object, such as a piece of text, is the length of a shortest computer program that produces the object as output. It is a measure of the computational resources needed to specify the object, and is also known as algorithmic complexity, Solomonoff–Kolmogorov–Chaitin complexity, program-size complexity, descriptive complexity, or algorithmic entropy. It is named after Andrey Kolmogorov, who first published on the subject in 1963 and is a generalization of classical information theory.
In the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that, informally speaking, represents the probability that a randomly constructed program will halt. These numbers are formed from a construction due to Gregory Chaitin.

In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".
Information theory is the mathematical study of the quantification, storage, and communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field, in applied mathematics, is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering, and electrical engineering.
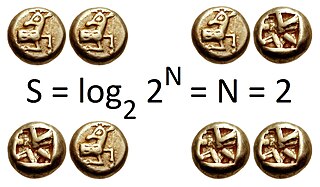
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable , which takes values in the alphabet and is distributed according to , the entropy is
In digital transmission, the number of bit errors is the number of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.

In information theory, the Hamming distance between two strings or vectors of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of substitutions required to change one string into the other, or equivalently, the minimum number of errors that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences. It is named after the American mathematician Richard Hamming.
A binary symmetric channel is a common communications channel model used in coding theory and information theory. In this model, a transmitter wishes to send a bit, and the receiver will receive a bit. The bit will be "flipped" with a "crossover probability" of p, and otherwise is received correctly. This model can be applied to varied communication channels such as telephone lines or disk drive storage.
Rate–distortion theory is a major branch of information theory which provides the theoretical foundations for lossy data compression; it addresses the problem of determining the minimal number of bits per symbol, as measured by the rate R, that should be communicated over a channel, so that the source can be approximately reconstructed at the receiver without exceeding an expected distortion D.
Channel capacity, in electrical engineering, computer science, and information theory, is the theoretical maximum rate at which information can be reliably transmitted over a communication channel.

Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data.
In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here, "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems. Not being one-to-one is not considered sufficient for a function to be called one-way.

In algorithmic information theory, algorithmic probability, also known as Solomonoff probability, is a mathematical method of assigning a prior probability to a given observation. It was invented by Ray Solomonoff in the 1960s. It is used in inductive inference theory and analyses of algorithms. In his general theory of inductive inference, Solomonoff uses the method together with Bayes' rule to obtain probabilities of prediction for an algorithm's future outputs.
The Wedderburn–Etherington numbers are an integer sequence named for Ivor Malcolm Haddon Etherington and Joseph Wedderburn that can be used to count certain kinds of binary trees. The first few numbers in the sequence are
In information theory, Shannon's source coding theorem establishes the statistical limits to possible data compression for data whose source is an independent identically-distributed random variable, and the operational meaning of the Shannon entropy.
In coding theory, decoding is the process of translating received messages into codewords of a given code. There have been many common methods of mapping messages to codewords. These are often used to recover messages sent over a noisy channel, such as a binary symmetric channel.
In information theory, the noisy-channel coding theorem, establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data nearly error-free up to a computable maximum rate through the channel. This result was presented by Claude Shannon in 1948 and was based in part on earlier work and ideas of Harry Nyquist and Ralph Hartley.

In coding theory and information theory, a binary erasure channel (BEC) is a communications channel model. A transmitter sends a bit, and the receiver either receives the bit correctly, or with some probability receives a message that the bit was not received ("erased").

In coding theory and information theory, a Z-channel or binary asymmetric channel is a communications channel used to model the behaviour of some data storage systems.
In information theory, the interference channel is the basic model used to analyze the effect of interference in communication channels. The model consists of two pairs of users communicating through a shared channel. The problem of interference between two mobile users in close proximity or crosstalk between two parallel landlines are two examples where this model is applicable.