
A machine is a physical system using power to apply forces and control movement to perform an action. The term is commonly applied to artificial devices, such as those employing engines or motors, but also to natural biological macromolecules, such as molecular machines. Machines can be driven by animals and people, by natural forces such as wind and water, and by chemical, thermal, or electrical power, and include a system of mechanisms that shape the actuator input to achieve a specific application of output forces and movement. They can also include computers and sensors that monitor performance and plan movement, often called mechanical systems.

Origami is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a finished sculpture through folding and sculpting techniques. Modern origami practitioners generally discourage the use of cuts, glue, or markings on the paper. Origami folders often use the Japanese word kirigami to refer to designs which use cuts.
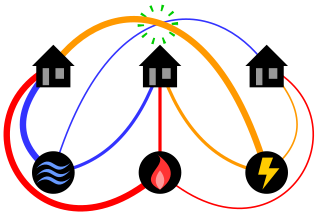
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.

The discipline of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability, and the use of paper folds to solve up-to cubic mathematical equations.
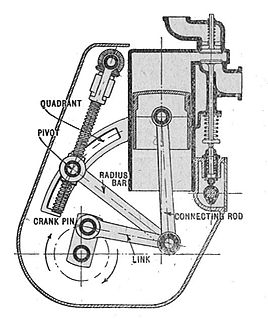
A mechanical linkage is an assembly of systems connected to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for example, and are called joints. A linkage modeled as a network of rigid links and ideal joints is called a kinematic chain.
The Ullmann reaction or Ullmann coupling is a coupling reaction between aryl halides. Traditionally this reaction is effected by copper, but palladium and nickel are also effective catalysts. The reaction is named after Fritz Ullmann.
Cell migration is a central process in the development and maintenance of multicellular organisms. Tissue formation during embryonic development, wound healing and immune responses all require the orchestrated movement of cells in particular directions to specific locations. Cells often migrate in response to specific external signals, including chemical signals and mechanical signals. Errors during this process have serious consequences, including intellectual disability, vascular disease, tumor formation and metastasis. An understanding of the mechanism by which cells migrate may lead to the development of novel therapeutic strategies for controlling, for example, invasive tumour cells.

In mathematics, a developable surface is a smooth surface with zero Gaussian curvature. That is, it is a surface that can be flattened onto a plane without distortion. Conversely, it is a surface which can be made by transforming a plane. In three dimensions all developable surfaces are ruled surfaces. There are developable surfaces in four-dimensional space which are not ruled.
The carpenter's rule problem is a discrete geometry problem, which can be stated in the following manner: Can a simple planar polygon be moved continuously to a position where all its vertices are in convex position, so that the edge lengths and simplicity are preserved along the way? A closely related problem is to show that any non-self-crossing polygonal chain can be straightened, again by a continuous transformation that preserves edge distances and avoids crossings.

In geometry, an antiparallelogram is a type of self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but these pairs of sides are not in general parallel. Instead, sides in the longer pair cross each other as in a scissors mechanism. Antiparallelograms are also called contraparallelograms or crossed parallelograms.

A straight-line mechanism is a mechanism that converts any type of rotary or angular motion to perfect or near-perfect straight-line motion, or vice-versa. Straight-line motion is linear motion of definite length or "stroke", every forward stroke being followed by a return stroke, giving reciprocating motion. The first such mechanism, patented in 1784 by James Watt, produced approximate straight-line motion, referred to by Watt as parallel motion.

In mechanical engineering, a compliant mechanism is a flexible mechanism that achieves force and motion transmission through elastic body deformation. It gains some or all of its motion from the relative flexibility of its members rather than from rigid-body joints alone. These may be monolithic (single-piece) or jointless structures. Some common devices that use compliant mechanisms are backpack latches and paper clips. One of the oldest examples of using compliant structures is the bow and arrow.

In geometry, a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897. The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces. These octahedra were the first flexible polyhedra to be discovered.

In engineering, a mechanism is a device that transforms input forces and movement into a desired set of output forces and movement. Mechanisms generally consist of moving components which may include:

The Birch reduction is an organic reaction that is used to convert arenes to cyclohexadienes. The reaction is named after the Australian chemist Arthur Birch and involves the organic reduction of aromatic rings in an amine solvent with an alkali metal and a proton source. Unlike catalytic hydrogenation, Birch reduction does not reduce the aromatic ring all the way to a cyclohexane.

Jansen's linkage is a planar leg mechanism designed by the kinetic sculptor Theo Jansen to generate a smooth walking motion. Jansen has used his mechanism in a variety of kinetic sculptures which are known as Strandbeesten. Jansen's linkage bears artistic as well as mechanical merit for its simulation of organic walking motion using a simple rotary input. These leg mechanisms have applications in mobile robotics and in gait analysis.
The sliding criterion (discontinuity) is a tool to estimate easily the shear strength properties of a discontinuity in a rock mass based on visual and tactile characterization of the discontinuity. The shear strength of a discontinuity is important in, for example, tunnel, foundation, or slope engineering, but also stability of natural slopes is often governed by the shear strength along discontinuities.
Lamina Emergent Mechanisms are more commonly referred to as "Pop-up Mechanisms" as seen in "pop-up-books". LEM is the technical term of such mechanisms or engineering. LEMs are a subset of compliant mechanisms fabricated from planar materials (lamina) and have motion emerging from the fabrication plane. LEMs use compliance, or the deflection of flexible members to achieve motion.
Larry L. Howell is a professor and Associate Academic Vice President (AAVP) at Brigham Young University (BYU). His research focuses on compliant mechanisms, including origami-inspired mechanisms, microelectromechanical systems, medical devices, space mechanisms, and developable mechanisms. Howell has also conducted research in lamina emergent mechanisms and nanoinjection. He received a bachelor's degree in mechanical engineering from BYU and master's and Ph.D. degrees from Purdue University. His Ph.D. advisor was Ashok Midha, who is regarded as the "Father of Compliant Mechanisms."

A Hoberman mechanism, or Hoberman linkage, is a deployable mechanism that turns linear motion into radial motion.















