
In mathematics, a group is a non-empty set with an operation that satisfies the following constraints: the operation is associative, has an identity element, and every element of the set has an inverse element.

In abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.

In mathematics, the Klein four-group is an abelian group with four elements, in which each element is self-inverse (composing it with itself produces the identity) and in which composing any two of the three non-identity elements produces the third one. It can be described as the symmetry group of a non-square rectangle (with the three non-identity elements being horizontal and vertical reflection and 180-degree rotation), as the group of bitwise exclusive or operations on two-bit binary values, or more abstractly as Z2 × Z2, the direct product of two copies of the cyclic group of order 2. It was named Vierergruppe (meaning four-group) by Felix Klein in 1884. It is also called the Klein group, and is often symbolized by the letter V or as K4.

In group theory, a branch of abstract algebra in pure mathematics, a cyclic group or monogenous group is a group, denoted Cn, that is generated by a single element. That is, it is a set of invertible elements with a single associative binary operation, and it contains an element g such that every other element of the group may be obtained by repeatedly applying the group operation to g or its inverse. Each element can be written as an integer power of g in multiplicative notation, or as an integer multiple of g in additive notation. This element g is called a generator of the group.

In abstract algebra, a generating set of a group is a subset of the group set such that every element of the group can be expressed as a combination of finitely many elements of the subset and their inverses.

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups, and finite Coxeter groups were classified in 1935.

In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem, and uses a specified set of generators for the group. It is a central tool in combinatorial and geometric group theory. The structure and symmetry of Cayley graphs makes them particularly good candidates for constructing families of expander graphs.
In the mathematical field of graph theory, a vertex-transitive graph is a graph G in which, given any two vertices v1 and v2 of G, there is some automorphism
In the mathematical area of group theory, Artin groups, also known as Artin–Tits groups or generalized braid groups, are a family of infinite discrete groups defined by simple presentations. They are closely related with Coxeter groups. Examples are free groups, free abelian groups, braid groups, and right-angled Artin–Tits groups, among others.
The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.

In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a word hyperbolic group or Gromov hyperbolic group, is a finitely generated group equipped with a word metric satisfying certain properties abstracted from classical hyperbolic geometry. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov (1987). The inspiration came from various existing mathematical theories: hyperbolic geometry but also low-dimensional topology, and combinatorial group theory. In a very influential chapter from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow, William Thurston, James W. Cannon, Eliyahu Rips, and many others.

László "Laci" Babai is a Hungarian professor of computer science and mathematics at the University of Chicago. His research focuses on computational complexity theory, algorithms, combinatorics, and finite groups, with an emphasis on the interactions between these fields.
In graph theory, the Lovász conjecture (1969) is a classical problem on Hamiltonian paths in graphs. It says:
In mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group. The motivating examples of relatively hyperbolic groups are the fundamental groups of complete noncompact hyperbolic manifolds of finite volume.
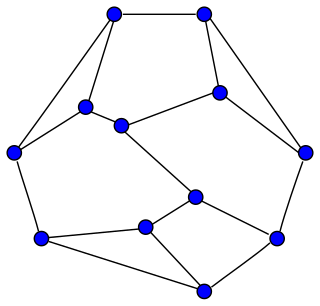
Frucht's theorem is a theorem in algebraic graph theory conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph. More strongly, for any finite group G there exist infinitely many non-isomorphic simple connected graphs such that the automorphism group of each of them is isomorphic to G.
László Pyber is a Hungarian mathematician. He is a researcher at the Alfréd Rényi Institute of Mathematics, Budapest. He works in combinatorics and group theory.

In computational group theory, a black box group is a group G whose elements are encoded by bit strings of length N, and group operations are performed by an oracle. These operations include:
Babai's problem is a problem in algebraic graph theory first proposed in 1979 by László Babai.











