In game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. More specifically, a state variable or variables evolve over time according to a differential equation. Early analyses reflected military interests, considering two actors—the pursuer and the evader—with diametrically opposed goals. More recent analyses have reflected engineering or economic considerations. [1] [2]
Differential games are related closely with optimal control problems. In an optimal control problem there is single control and a single criterion to be optimized; differential game theory generalizes this to two controls and two criteria, one for each player. [3] Each player attempts to control the state of the system so as to achieve its goal; the system responds to the inputs of all players.
In the study of competition, differential games have been employed since a 1925 article by Charles F. Roos. [4] The first to study the formal theory of differential games was Rufus Isaacs, publishing a text-book treatment in 1965. [5] One of the first games analyzed was the 'homicidal chauffeur game'.
Games with a random time horizon are a particular case of differential games. [6] In such games, the terminal time is a random variable with a given probability distribution function. Therefore, the players maximize the mathematical expectancy of the cost function. It was shown that the modified optimization problem can be reformulated as a discounted differential game over an infinite time interval [7] [8]
Differential games have been applied to economics. Recent developments include adding stochasticity to differential games and the derivation of the stochastic feedback Nash equilibrium (SFNE). A recent example is the stochastic differential game of capitalism by Leong and Huang (2010). [9] In 2016 Yuliy Sannikov received the John Bates Clark Medal from the American Economic Association for his contributions to the analysis of continuous-time dynamic games using stochastic calculus methods. [10] [11]
Additionally, differential games have applications in missile guidance [12] [13] and autonomous systems. [14]
For a survey of pursuit–evasion differential games see Pachter. [15]
Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
Optimal control theory is a branch of mathematical optimization that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory.
The Hamilton-Jacobi-Bellman (HJB) equation is a nonlinear partial differential equation that provides necessary and sufficient conditions for optimality of a control with respect to a loss function. Its solution is the value function of the optimal control problem which, once known, can be used to obtain the optimal control by taking the maximizer of the Hamiltonian involved in the HJB equation.
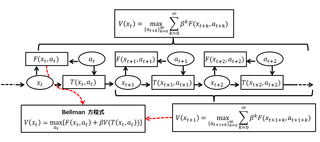
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.
Trajectory optimization is the process of designing a trajectory that minimizes some measure of performance while satisfying a set of constraints. Generally speaking, trajectory optimization is a technique for computing an open-loop solution to an optimal control problem. It is often used for systems where computing the full closed-loop solution is not required, impractical or impossible. If a trajectory optimization problem can be solved at a rate given by the inverse of the Lipschitz constant, then it can be used iteratively to generate a closed-loop solution in the sense of Caratheodory. If only the first step of the trajectory is executed for an infinite-horizon problem, then this is known as Model Predictive Control (MPC).
A princess and monster game is a pursuit–evasion game played by two players in a region.
Pseudospectral optimal control is a joint theoretical-computational method for solving optimal control problems. It combines pseudospectral (PS) theory with optimal control theory to produce PS optimal control theory. PS optimal control theory has been used in ground and flight systems in military and industrial applications. The techniques have been extensively used to solve a wide range of problems such as those arising in UAV trajectory generation, missile guidance, control of robotic arms, vibration damping, lunar guidance, magnetic control, swing-up and stabilization of an inverted pendulum, orbit transfers, tether libration control, ascent guidance and quantum control.
DIDO is a MATLAB optimal control toolbox for solving general-purpose optimal control problems. It is widely used in academia, industry, and NASA. Hailed as a breakthrough software, DIDO is based on the pseudospectral optimal control theory of Ross and Fahroo. The latest enhancements to DIDO are described in Ross.
Stochastic control or stochastic optimal control is a sub field of control theory that deals with the existence of uncertainty either in observations or in the noise that drives the evolution of the system. The system designer assumes, in a Bayesian probability-driven fashion, that random noise with known probability distribution affects the evolution and observation of the state variables. Stochastic control aims to design the time path of the controlled variables that performs the desired control task with minimum cost, somehow defined, despite the presence of this noise. The context may be either discrete time or continuous time.
Yu-Chi "Larry" Ho is a Chinese-American mathematician, control theorist, and a professor at the School of Engineering and Applied Sciences, Harvard University.
The Sethi model was developed by Suresh P. Sethi and describes the process of how sales evolve over time in response to advertising. The model assumes that the rate of change in sales depend on three effects: response to advertising that acts positively on the unsold portion of the market, the loss due to forgetting or possibly due to competitive factors that act negatively on the sold portion of the market, and a random effect that can go either way.
The Chebyshev pseudospectral method for optimal control problems is based on Chebyshev polynomials of the first kind. It is part of the larger theory of pseudospectral optimal control, a term coined by Ross. Unlike the Legendre pseudospectral method, the Chebyshev pseudospectral (PS) method does not immediately offer high-accuracy quadrature solutions. Consequently, two different versions of the method have been proposed: one by Elnagar et al., and another by Fahroo and Ross. The two versions differ in their quadrature techniques. The Fahroo–Ross method is more commonly used today due to the ease in implementation of the Clenshaw–Curtis quadrature technique. In 2008, Trefethen showed that the Clenshaw–Curtis method was nearly as accurate as Gauss quadrature. This breakthrough result opened the door for a covector mapping theorem for Chebyshev PS methods. A complete mathematical theory for Chebyshev PS methods was finally developed in 2009 by Gong, Ross and Fahroo.
Introduced by I. Michael Ross and F. Fahroo, the Ross–Fahroo pseudospectral methods are a broad collection of pseudospectral methods for optimal control. Examples of the Ross–Fahroo pseudospectral methods are the pseudospectral knotting method, the flat pseudospectral method, the Legendre-Gauss-Radau pseudospectral method and pseudospectral methods for infinite-horizon optimal control.
The Bellman pseudospectral method is a pseudospectral method for optimal control based on Bellman's principle of optimality. It is part of the larger theory of pseudospectral optimal control, a term coined by Ross. The method is named after Richard E. Bellman. It was introduced by Ross et al. first as a means to solve multiscale optimal control problems, and later expanded to obtain suboptimal solutions for general optimal control problems.
Isaac Michael Ross is a Distinguished Professor and Program Director of Control and Optimization at the Naval Postgraduate School in Monterey, CA. He has published a highly-regarded textbook on optimal control theory and seminal papers in pseudospectral optimal control theory, energy-sink theory, the optimization and deflection of near-Earth asteroids and comets, robotics, attitude dynamics and control, orbital mechanics, real-time optimal control and unscented optimal control. The Kang–Ross–Gong theorem, Ross' π lemma, Ross' time constant, the Ross–Fahroo lemma, and the Ross–Fahroo pseudospectral method are all named after him.
Mean-field game theory is the study of strategic decision making by small interacting agents in very large populations. It lies at the intersection of game theory with stochastic analysis and control theory. The use of the term "mean field" is inspired by mean-field theory in physics, which considers the behavior of systems of large numbers of particles where individual particles have negligible impacts upon the system. In other words, each agent acts according to his minimization or maximization problem taking into account other agents’ decisions and because their population is large we can assume the number of agents goes to infinity and a representative agent exists.
Vivek Shripad Borkar is an Indian electrical engineer, mathematician and an Institute chair professor at the Indian Institute of Technology, Mumbai. He is known for introducing analytical paradigm in stochastic optimal control processes and is an elected fellow of all the three major Indian science academies viz. the Indian Academy of Sciences, Indian National Science Academy and the National Academy of Sciences, India. He also holds elected fellowships of The World Academy of Sciences, Institute of Electrical and Electronics Engineers, Indian National Academy of Engineering and the American Mathematical Society. The Council of Scientific and Industrial Research, the apex agency of the Government of India for scientific research, awarded him the Shanti Swarup Bhatnagar Prize for Science and Technology, one of the highest Indian science awards for his contributions to Engineering Sciences in 1992. He received the TWAS Prize of the World Academy of Sciences in 2009.
In mathematics, unscented optimal control combines the notion of the unscented transform with deterministic optimal control to address a class of uncertain optimal control problems. It is a specific application of Riemmann-Stieltjes optimal control theory, a concept introduced by Ross and his coworkers.
Hamidou Tembine is a French game theorist and researcher specializing in evolutionary games and co-opetitive mean-field-type games. He has been a Global Network Assistant Professor at New York University. He has been also the principal investigator and director of the Game Theory and Learning Laboratory at New York University.
Probabilistic numerics is an active field of study at the intersection of applied mathematics, statistics, and machine learning centering on the concept of uncertainty in computation. In probabilistic numerics, tasks in numerical analysis such as finding numerical solutions for integration, linear algebra, optimization and simulation and differential equations are seen as problems of statistical, probabilistic, or Bayesian inference.
