Distensibility is a metric of the stiffness of blood vessels. It is defined as
,
where and are the diameter of the vessel in systole and diastole, and and are the systolic and diastolic blood pressure. [1]
Distensibility is a metric of the stiffness of blood vessels. It is defined as
,
where and are the diameter of the vessel in systole and diastole, and and are the systolic and diastolic blood pressure. [1]

Blood pressure (BP) is the pressure of circulating blood against the walls of blood vessels. Most of this pressure results from the heart pumping blood through the circulatory system. When used without qualification, the term "blood pressure" refers to the pressure in a brachial artery, where it is most commonly measured. Blood pressure is usually expressed in terms of the systolic pressure over diastolic pressure in the cardiac cycle. It is measured in millimeters of mercury (mmHg) above the surrounding atmospheric pressure, or in kilopascals (kPa). The difference between the systolic and diastolic pressures is known as pulse pressure, while the average pressure during a cardiac cycle is known as mean arterial pressure.

In numerical analysis, the Runge–Kutta methods are a family of implicit and explicit iterative methods, which include the Euler method, used in temporal discretization for the approximate solutions of simultaneous nonlinear equations. These methods were developed around 1900 by the German mathematicians Carl Runge and Wilhelm Kutta.
Hemodynamics or haemodynamics are the dynamics of blood flow. The circulatory system is controlled by homeostatic mechanisms of autoregulation, just as hydraulic circuits are controlled by control systems. The hemodynamic response continuously monitors and adjusts to conditions in the body and its environment. Hemodynamics explains the physical laws that govern the flow of blood in the blood vessels.

Soft tissue connects and surrounds or supports internal organs and bones, and includes muscle, tendons, ligaments, fat, fibrous tissue, lymph and blood vessels, fasciae, and synovial membranes. Soft tissue is tissue in the body that is not hardened by the processes of ossification or calcification such as bones and teeth.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.
Hemorheology, also spelled haemorheology, or blood rheology, is the study of flow properties of blood and its elements of plasma and cells. Proper tissue perfusion can occur only when blood's rheological properties are within certain levels. Alterations of these properties play significant roles in disease processes. Blood viscosity is determined by plasma viscosity, hematocrit and mechanical properties of red blood cells. Red blood cells have unique mechanical behavior, which can be discussed under the terms erythrocyte deformability and erythrocyte aggregation. Because of that, blood behaves as a non-Newtonian fluid. As such, the viscosity of blood varies with shear rate. Blood becomes less viscous at high shear rates like those experienced with increased flow such as during exercise or in peak-systole. Therefore, blood is a shear-thinning fluid. Contrarily, blood viscosity increases when shear rate goes down with increased vessel diameters or with low flow, such as downstream from an obstruction or in diastole. Blood viscosity also increases with increases in red cell aggregability.

Fluid statics or hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body".
Vascular resistance is the resistance that must be overcome for blood to flow through the circulatory system. The resistance offered by the systemic circulation is known as the systemic vascular resistance (SVR) or may sometimes be called by the older term total peripheral resistance (TPR), while the resistance offered by the pulmonary circulation is known as the pulmonary vascular resistance (PVR). Vasoconstriction increases resistance, whereas vasodilation decreases resistance. Blood flow and cardiac function is related to blood pressure and inversely related to vascular resistance.
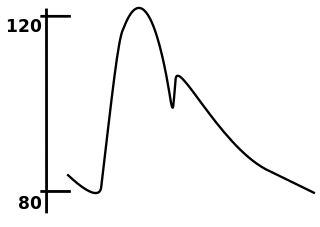
In medicine, the mean arterial pressure (MAP) is an average calculated blood pressure in an individual during a single cardiac cycle. Although methods of estimating MAP vary, a common calculation is to take one-third of the pulse pressure, and add that amount to the diastolic pressure. A normal MAP is about 90 mmHg.
Compliance is the ability of a hollow organ (vessel) to distend and increase volume with increasing transmural pressure or the tendency of a hollow organ to resist recoil toward its original dimensions on application of a distending or compressing force. It is the reciprocal of "elastance", hence elastance is a measure of the tendency of a hollow organ to recoil toward its original dimensions upon removal of a distending or compressing force.
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proven difficult to formulate a precise definition of stiffness, but the main idea is that the equation includes some terms that can lead to rapid variation in the solution.
The isothermal–isobaric ensemble is a statistical mechanical ensemble that maintains constant temperature and constant pressure applied. It is also called the -ensemble, where the number of particles is also kept as a constant. This ensemble plays an important role in chemistry as chemical reactions are usually carried out under constant pressure condition. The NPT ensemble is also useful for measuring the equation of state of model systems whose virial expansion for pressure cannot be evaluated, or systems near first-order phase transitions.
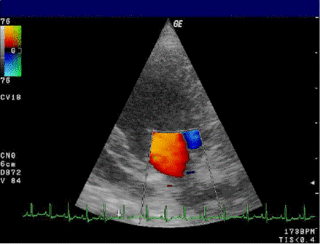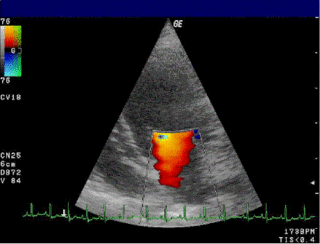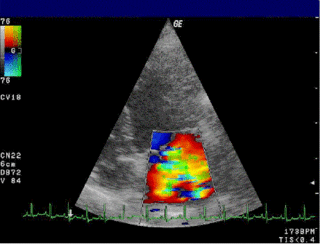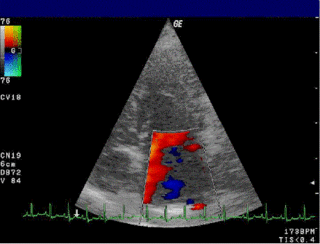
Doppler echocardiography is a procedure that uses Doppler ultrasonography to examine the heart. An echocardiogram uses high frequency sound waves to create an image of the heart while the use of Doppler technology allows determination of the speed and direction of blood flow by utilizing the Doppler effect.
In probability and statistics, the Tweedie distributions are a family of probability distributions which include the purely continuous normal, gamma and inverse Gaussian distributions, the purely discrete scaled Poisson distribution, and the class of compound Poisson–gamma distributions which have positive mass at zero, but are otherwise continuous. Tweedie distributions are a special case of exponential dispersion models and are often used as distributions for generalized linear models.

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix is a matrix that represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation.
Pulse wave velocity (PWV) is the velocity at which the blood pressure pulse propagates through the circulatory system, usually an artery or a combined length of arteries. PWV is used clinically as a measure of arterial stiffness and can be readily measured non-invasively in humans, with measurement of carotid to femoral PWV (cfPWV) being the recommended method. cfPWV is highly reproducible, and predicts future cardiovascular events and all-cause mortality independent of conventional cardiovascular risk factors. It has been recognized by the European Society of Hypertension as an indicator of target organ damage and a useful additional test in the investigation of hypertension.

Magnetic levitation (maglev) or magnetic suspension is a method by which an object is suspended with no support other than magnetic fields. Magnetic force is used to counteract the effects of the gravitational force and any other forces.
Quantum stochastic calculus is a generalization of stochastic calculus to noncommuting variables. The tools provided by quantum stochastic calculus are of great use for modeling the random evolution of systems undergoing measurement, as in quantum trajectories. Just as the Lindblad master equation provides a quantum generalization to the Fokker–Planck equation, quantum stochastic calculus allows for the derivation of quantum stochastic differential equations (QSDE) that are analogous to classical Langevin equations.
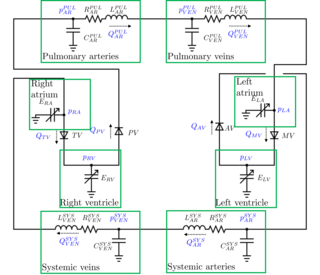
A lumped parameter cardiovascular model is a zero-dimensional mathematical model used to describe the hemodynamics of the cardiovascular system. Given a set of parameters that have a physical meaning, it allows to study the changes in blood pressures or flow rates throughout the cardiovascular system. Modifying the parameters, it is possible to study the effects of a specific disease. For example, arterial hypertension is modeled increasing the arterial resistances of the model.