Related Research Articles

A chemical bond is the association of atoms or ions to form molecules, crystals, and other structures. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds or through the sharing of electrons as in covalent bonds, or some combination of these effects. Chemical bonds are described as having different strengths: there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force, and hydrogen bonding.

In physics, a dipole is an electromagnetic phenomenon which occurs in two ways:
An intermolecular force (IMF) is the force that mediates interaction between molecules, including the electromagnetic forces of attraction or repulsion which act between atoms and other types of neighbouring particles, e.g. atoms or ions. Intermolecular forces are weak relative to intramolecular forces – the forces which hold a molecule together. For example, the covalent bond, involving sharing electron pairs between atoms, is much stronger than the forces present between neighboring molecules. Both sets of forces are essential parts of force fields frequently used in molecular mechanics.
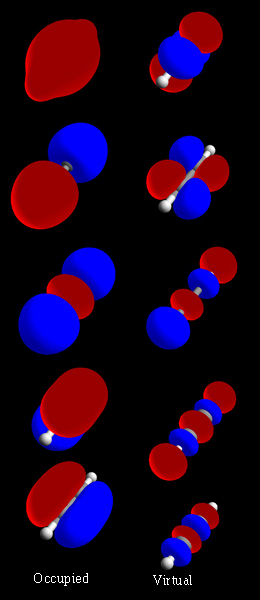
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms atomic orbital and molecular orbital were introduced by Robert S. Mulliken in 1932 to mean one-electron orbital wave functions. At an elementary level, they are used to describe the region of space in which a function has a significant amplitude.

In molecular physics and chemistry, the van der Waals force is a distance-dependent interaction between atoms or molecules. Unlike ionic or covalent bonds, these attractions do not result from a chemical electronic bond; they are comparatively weak and therefore more susceptible to disturbance. The van der Waals force quickly vanishes at longer distances between interacting molecules.

Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics.

London dispersion forces are a type of intermolecular force acting between atoms and molecules that are normally electrically symmetric; that is, the electrons are symmetrically distributed with respect to the nucleus. They are part of the van der Waals forces. The LDF is named after the German physicist Fritz London. They are the weakest intermolecular force.
In physics and chemistry, a selection rule, or transition rule, formally constrains the possible transitions of a system from one quantum state to another. Selection rules have been derived for electromagnetic transitions in molecules, in atoms, in atomic nuclei, and so on. The selection rules may differ according to the technique used to observe the transition. The selection rule also plays a role in chemical reactions, where some are formally spin-forbidden reactions, that is, reactions where the spin state changes at least once from reactants to products.
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system for three-dimensional Euclidean space, . Similarly to Taylor series, multipole expansions are useful because oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on , or less often on for some other .
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.
In theoretical and computational chemistry, a basis set is a set of functions that is used to represent the electronic wave function in the Hartree–Fock method or density-functional theory in order to turn the partial differential equations of the model into algebraic equations suitable for efficient implementation on a computer.
Mulliken charges arise from the Mulliken population analysis and provide a means of estimating partial atomic charges from calculations carried out by the methods of computational chemistry, particularly those based on the linear combination of atomic orbitals molecular orbital method, and are routinely used as variables in linear regression (QSAR) procedures. The method was developed by Robert S. Mulliken, after whom the method is named. If the coefficients of the basis functions in the molecular orbital are Cμi for the μ'th basis function in the i'th molecular orbital, the density matrix terms are:
In chemistry, a non-covalent interaction differs from a covalent bond in that it does not involve the sharing of electrons, but rather involves more dispersed variations of electromagnetic interactions between molecules or within a molecule. The chemical energy released in the formation of non-covalent interactions is typically on the order of 1–5 kcal/mol. Non-covalent interactions can be classified into different categories, such as electrostatic, π-effects, van der Waals forces, and hydrophobic effects.

SIESTA is an original method and its computer program implementation, to efficiently perform electronic structure calculations and ab initio molecular dynamics simulations of molecules and solids. SIESTA uses strictly localized basis sets and the implementation of linear-scaling algorithms. Accuracy and speed can be set in a wide range, from quick exploratory calculations to highly accurate simulations matching the quality of other approaches, such as the plane-wave and all-electron methods.
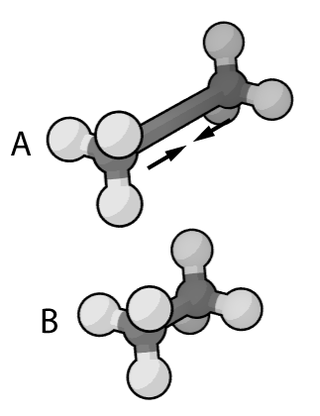
In the context of chemistry, molecular physics, physical chemistry, and molecular modelling, a force field is a computational model that is used to describe the forces between atoms within molecules or between molecules as well as in crystals. Force fields are a variety of interatomic potentials. More precisely, the force field refers to the functional form and parameter sets used to calculate the potential energy of a system on the atomistic level. Force fields are usually used in molecular dynamics or Monte Carlo simulations. The parameters for a chosen energy function may be derived from classical laboratory experiment data, calculations in quantum mechanics, or both. Force fields utilize the same concept as force fields in classical physics, with the main difference being that the force field parameters in chemistry describe the energy landscape on the atomistic level. From a force field, the acting forces on every particle are derived as a gradient of the potential energy with respect to the particle coordinates.

In chemistry, pi stacking refers to the presumptive attractive, noncovalent pi interactions between the pi bonds of aromatic rings. However this is a misleading description of the phenomena since direct stacking of aromatic rings is electrostatically repulsive. What is more commonly observed is either a staggered stacking or pi-teeing interaction both of which are electrostatic attractive For example, the most commonly observed interactions between aromatic rings of amino acid residues in proteins is a staggered stacked followed by a perpendicular orientation. Sandwiched orientations are relatively rare.

PQS is a general purpose quantum chemistry program. Its roots go back to the first ab initio gradient program developed in Professor Peter Pulay's group but now it is developed and distributed commercially by Parallel Quantum Solutions. There is a reduction in cost for academic users and a site license. Its strong points are geometry optimization, NMR chemical shift calculations, and large MP2 calculations, and high parallel efficiency on computing clusters. It includes many other capabilities including Density functional theory, the semiempirical methods, MINDO/3, MNDO, AM1 and PM3, Molecular mechanics using the SYBYL 5.0 Force Field, the quantum mechanics/molecular mechanics mixed method using the ONIOM method, natural bond orbital (NBO) analysis and COSMO solvation models. Recently, a highly efficient parallel CCSD(T) code for closed shell systems has been developed. This code includes many other post Hartree–Fock methods: MP2, MP3, MP4, CISD, CEPA, QCISD and so on.

A molecular solid is a solid consisting of discrete molecules. The cohesive forces that bind the molecules together are van der Waals forces, dipole–dipole interactions, quadrupole interactions, π–π interactions, hydrogen bonding, halogen bonding, London dispersion forces, and in some molecular solids, coulombic interactions. Van der Waals, dipole interactions, quadrupole interactions, π–π interactions, hydrogen bonding, and halogen bonding are typically much weaker than the forces holding together other solids: metallic, ionic, and network solids. Intermolecular interactions typically do not involve delocalized electrons, unlike metallic and certain covalent bonds. Exceptions are charge-transfer complexes such as the tetrathiafulvane-tetracyanoquinodimethane (TTF-TCNQ), a radical ion salt. These differences in the strength of force and electronic characteristics from other types of solids give rise to the unique mechanical, electronic, and thermal properties of molecular solids.

In computational chemistry, a water model is used to simulate and thermodynamically calculate water clusters, liquid water, and aqueous solutions with explicit solvent. The models are determined from quantum mechanics, molecular mechanics, experimental results, and these combinations. To imitate a specific nature of molecules, many types of models have been developed. In general, these can be classified by the following three points; (i) the number of interaction points called site, (ii) whether the model is rigid or flexible, (iii) whether the model includes polarization effects.
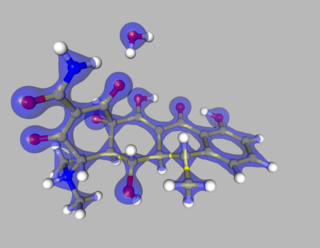
The Multipole Density Formalism is an X-ray crystallography method of electron density modelling proposed by Niels K. Hansen and Philip Coppens in 1978. Unlike the commonly used Independent Atom Model, the Hansen-Coppens Formalism presents an aspherical approach, allowing one to model the electron distribution around a nucleus separately in different directions and therefore describe numerous chemical features of a molecule inside the unit cell of an examined crystal in detail.
References
- ↑ Stone, A.J.; Alderton, M. (1985). "Distributed multipole analysis methods and applications". Molecular Physics. 56 (5): 1047–1064. Bibcode:1985MolPh..56.1047S. doi:10.1080/00268978500102891.
- ↑ Rein, R. (1973). "On Physical Properties and Interactions of Polyatomic Molecules: With Application to Molecular Recognition in Biology". Advances in Quantum Chemistry. 7: 335–396. Bibcode:1973AdQC....7..335R. doi:10.1016/S0065-3276(08)60568-7. ISBN 9780120348077.
- ↑ Boys, S. F.; Egerton, Alfred Charles (1950-02-22). "Electronic wave functions - I. A general method of calculation for the stationary states of any molecular system". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 200 (1063): 542–554. Bibcode:1950RSPSA.200..542B. doi:10.1098/rspa.1950.0036. S2CID 122709395.
- ↑ Ponder, Jay W.; Wu, Chuanjie; Ren, Pengyu; Pande, Vijay S.; Chodera, John D.; Schnieders, Michael J.; Haque, Imran; Mobley, David L.; Lambrecht, Daniel S.; DiStasio, Robert A.; Head-Gordon, Martin; Clark, Gary N. I.; Johnson, Margaret E.; Head-Gordon, Teresa (4 March 2010). "Current Status of the AMOEBA Polarizable Force Field". The Journal of Physical Chemistry B. 114 (8): 2549–2564. doi:10.1021/jp910674d. PMC 2918242 . PMID 20136072.