
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. The term vibration is precisely used to describe mechanical oscillation. Familiar examples of oscillation include a swinging pendulum and alternating current.

In the physical sciences, a phase is a region of space, throughout which all physical properties of a material are essentially uniform. Examples of physical properties include density, index of refraction, magnetization and chemical composition. A simple description is that a phase is a region of material that is chemically uniform, physically distinct, and (often) mechanically separable. In a system consisting of ice and water in a glass jar, the ice cubes are one phase, the water is a second phase, and the humid air is a third phase over the ice and water. The glass of the jar is another separate phase.
Statics is the branch of mechanics that is concerned with the analysis of loads acting on physical systems that do not experience an acceleration (a=0), but rather, are in static equilibrium with their environment. When in static equilibrium, the acceleration of the system is zero and the system is either at rest, or its center of mass moves at constant velocity. The application of Newton's second law to a system gives:
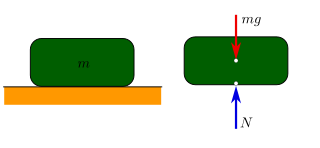
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is zero.
In economics, economic equilibrium is a situation in which economic forces such as supply and demand are balanced and in the absence of external influences the (equilibrium) values of economic variables will not change. For example, in the standard textbook model of perfect competition, equilibrium occurs at the point at which quantity demanded and quantity supplied are equal. Market equilibrium in this case is a condition where a market price is established through competition such that the amount of goods or services sought by buyers is equal to the amount of goods or services produced by sellers. This price is often called the competitive price or market clearing price and will tend not to change unless demand or supply changes, and the quantity is called the "competitive quantity" or market clearing quantity. However, the concept of equilibrium in economics also applies to imperfectly competitive markets, where it takes the form of a Nash equilibrium.
A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter.
Thermodynamic equilibrium is an axiomatic concept of thermodynamics. It is an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable walls. In thermodynamic equilibrium there are no net macroscopic flows of matter or of energy, either within a system or between systems. In a system in its own state of internal thermodynamic equilibrium, no macroscopic change occurs. Systems in mutual thermodynamic equilibrium are simultaneously in mutual thermal, mechanical, chemical, and radiative equilibria. Systems can be in one kind of mutual equilibrium, though not in others. In thermodynamic equilibrium, all kinds of equilibrium hold at once and indefinitely, until disturbed by a thermodynamic operation. In a macroscopic equilibrium, almost or perfectly exactly balanced microscopic exchanges occur; this is the physical explanation of the notion of macroscopic equilibrium.
Both headland and bay are two coastal features that are related and often found on the same coastline. A bay is a body of water—usually seawater and sometimes fresh water— mostly surrounded by land, whereas a headland is surrounded by water on three sides. Headlands are characterized by breaking waves, rocky shores, intense erosion and steep sea cliffs. Bays generally have less wave activity and typically have sandy beaches. Headlands and bays form on discordant coastlines, where the land consists of bands of rock of alternating resistance that run perpendicular to the coast.
In the theory of ordinary differential equations (ODEs), Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory of dynamical systems and control theory. A similar concept appears in the theory of general state space Markov chains, usually under the name Foster–Lyapunov functions.
In systems theory, a system or a process is in a steady state if the variables which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties p of the system, the partial derivative with respect to time is zero and remains so:

Michio Morishima was a Japanese economist, mathematician and econometrician, who was a faculty member at the London School of Economics from 1970–88 as the Sir John Hicks Professor of Economics. He was also emeritus professor of Osaka University and a member of the British Academy.
In ionic steady state, cells maintain different internal and external concentrations of various ionic species.

In the study of dynamical systems, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point that does not have any center manifolds. Near a hyperbolic point the orbits of a two-dimensional, non-dissipative system resemble hyperbolas. This fails to hold in general. Strogatz notes that "hyperbolic is an unfortunate name—it sounds like it should mean 'saddle point'—but it has become standard." Several properties hold about a neighborhood of a hyperbolic point, notably

In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later time as a result of the maximum principle. In partial differential equations one may measure the distances between functions using Lp norms or the sup norm, while in differential geometry one may measure the distance between spaces using the Gromov–Hausdorff distance.
In game theory, a subgame perfect equilibrium is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game. Informally, this means that if the players played any smaller game that consisted of only one part of the larger game, their behavior would represent a Nash equilibrium of that smaller game. Every finite extensive game has a subgame perfect equilibrium.
Restoring force, in a physics context, is a force that gives rise to an equilibrium in a physical system. If the system is perturbed away from the equilibrium, the restoring force will tend to bring the system back toward equilibrium. The restoring force is a function only of position of the mass or particle. It is always directed back toward the equilibrium position of the system. The restoring force is often referred to in simple harmonic motion. The force which is responsible to restore original size and shape is called restoring force.
Quasistatic approximation(s) refers to different domains and different meanings. In the most common acceptance, quasistatic approximation refers to equations that keep a static form even if some quantities are allowed to vary slowly with time. In electromagnetism it refers to mathematical models that can be used to describe devices that do not produce significant amounts of electromagnetic waves. For instance the capacitor and the coil in electrical networks.





