A duopoly is a type of oligopoly where two firms have dominant or exclusive control over a market, and most of the competition within that market occurs directly between them.
Microeconomics is a branch of economics that studies the behavior of individuals and firms in making decisions regarding the allocation of scarce resources and the interactions among these individuals and firms. Microeconomics focuses on the study of individual markets, sectors, or industries as opposed to the economy as a whole, which is studied in macroeconomics.
An oligopoly is a market in which pricing control lies in the hands of a few sellers.

In economics, specifically general equilibrium theory, a perfect market, also known as an atomistic market, is defined by several idealizing conditions, collectively called perfect competition, or atomistic competition. In theoretical models where conditions of perfect competition hold, it has been demonstrated that a market will reach an equilibrium in which the quantity supplied for every product or service, including labor, equals the quantity demanded at the current price. This equilibrium would be a Pareto optimum.

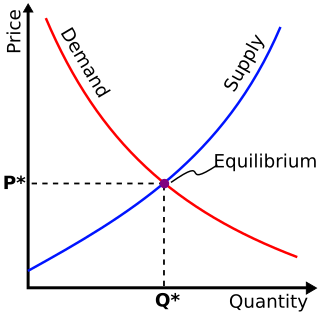
In microeconomics, supply and demand is an economic model of price determination in a market. It postulates that, holding all else equal, the unit price for a particular good or other traded item in a perfectly competitive market, will vary until it settles at the market-clearing price, where the quantity demanded equals the quantity supplied such that an economic equilibrium is achieved for price and quantity transacted. The concept of supply and demand forms the theoretical basis of modern economics.

This aims to be a complete article list of economics topics:

In economics, profit maximization is the short run or long run process by which a firm may determine the price, input and output levels that will lead to the highest possible total profit. In neoclassical economics, which is currently the mainstream approach to microeconomics, the firm is assumed to be a "rational agent" which wants to maximize its total profit, which is the difference between its total revenue and its total cost.
In economics, effective demand (ED) in a market is the demand for a product or service which occurs when purchasers are constrained in a different market. It contrasts with notional demand, which is the demand that occurs when purchasers are not constrained in any other market. In the aggregated market for goods in general, demand, notional or effective, is referred to as aggregate demand. The concept of effective supply parallels the concept of effective demand. The concept of effective demand or supply becomes relevant when markets do not continuously maintain equilibrium prices.
In economics, quantity adjustment is the process by which a market surplus leads to a cut-back in the quantity supplied or a market shortage causes an increase in supplied quantity. It is one possible result of supply and demand disequilibrium in a market. Quantity adjustment is complementary to pricing.

In economics, market clearing is the process by which, in an economic market, the supply of whatever is traded is equated to the demand so that there is no excess supply or demand, ensuring that there is neither a surplus nor a shortage. The new classical economics assumes that in any given market, assuming that all buyers and sellers have access to information and that there is no "friction" impeding price changes, prices constantly adjust up or down to ensure market clearing.

Marginal revenue is a central concept in microeconomics that describes the additional total revenue generated by increasing product sales by 1 unit. Marginal revenue is the increase in revenue from the sale of one additional unit of product, i.e., the revenue from the sale of the last unit of product. It can be positive or negative. Marginal revenue is an important concept in vendor analysis. To derive the value of marginal revenue, it is required to examine the difference between the aggregate benefits a firm received from the quantity of a good and service produced last period and the current period with one extra unit increase in the rate of production. Marginal revenue is a fundamental tool for economic decision making within a firm's setting, together with marginal cost to be considered.
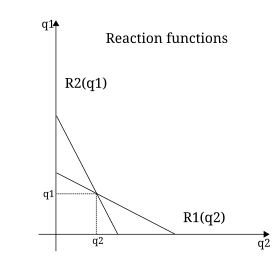
Bertrand competition is a model of competition used in economics, named after Joseph Louis François Bertrand (1822–1900). It describes interactions among firms (sellers) that set prices and their customers (buyers) that choose quantities at the prices set. The model was formulated in 1883 by Bertrand in a review of Antoine Augustin Cournot's book Recherches sur les Principes Mathématiques de la Théorie des Richesses (1838) in which Cournot had put forward the Cournot model. Cournot's model argued that each firm should maximise its profit by selecting a quantity level and then adjusting price level to sell that quantity. The outcome of the model equilibrium involved firms pricing above marginal cost; hence, the competitive price. In his review, Bertrand argued that each firm should instead maximise its profits by selecting a price level that undercuts its competitors' prices, when their prices exceed marginal cost. The model was not formalized by Bertrand; however, the idea was developed into a mathematical model by Francis Ysidro Edgeworth in 1889.
Cournot competition is an economic model used to describe an industry structure in which companies compete on the amount of output they will produce, which they decide on independently of each other and at the same time. It is named after Antoine Augustin Cournot (1801–1877) who was inspired by observing competition in a spring water duopoly. It has the following features:
The Stackelberg leadership model is a strategic game in economics in which the leader firm moves first and then the follower firms move sequentially. It is named after the German economist Heinrich Freiherr von Stackelberg who published Marktform und Gleichgewicht [Market Structure and Equilibrium] in 1934, which described the model. In game theory terms, the players of this game are a leader and a follower and they compete on quantity. The Stackelberg leader is sometimes referred to as the Market Leader.
Monetary disequilibrium theory is a product of the monetarist school and is mainly represented in the works of Leland Yeager and Austrian macroeconomics. The basic concepts of monetary equilibrium and disequilibrium were, however, defined in terms of an individual's demand for cash balance by Mises (1912) in his Theory of Money and Credit.

In economics, profit is the difference between revenue that an economic entity has received from its outputs and total costs of its inputs, also known as surplus value. It is equal to total revenue minus total cost, including both explicit and implicit costs.
The Brander–Spencer model is an economic model in international trade originally developed by James Brander and Barbara Spencer in the early 1980s. The model illustrates a situation where, under certain assumptions, a government can subsidize domestic firms to help them in their competition against foreign producers and in doing so enhances national welfare. This conclusion stands in contrast to results from most international trade models, in which government non-interference is socially optimal.
In oligopoly theory, conjectural variation is the belief that one firm has an idea about the way its competitors may react if it varies its output or price. The firm forms a conjecture about the variation in the other firm's output that will accompany any change in its own output. For example, in the classic Cournot model of oligopoly, it is assumed that each firm treats the output of the other firms as given when it chooses its output. This is sometimes called the "Nash conjecture," as it underlies the standard Nash equilibrium concept. However, alternative assumptions can be made. Suppose you have two firms producing the same good, so that the industry price is determined by the combined output of the two firms. Now suppose that each firm has what is called the "Bertrand Conjecture" of −1. This means that if firm A increases its output, it conjectures that firm B will reduce its output to exactly offset firm A's increase, so that total output and hence price remains unchanged. With the Bertrand Conjecture, the firms act as if they believe that the market price is unaffected by their own output, because each firm believes that the other firm will adjust its output so that total output will be constant. At the other extreme is the Joint-Profit maximizing conjecture of +1. In this case, each firm believes that the other will imitate exactly any change in output it makes, which leads to the firms behaving like a single monopoly supplier.
In microeconomics, the Bertrand–Edgeworth model of price-setting oligopoly looks at what happens when there is a homogeneous product where there is a limit to the output of firms which are willing and able to sell at a particular price. This differs from the Bertrand competition model where it is assumed that firms are willing and able to meet all demand. The limit to output can be considered as a physical capacity constraint which is the same at all prices, or to vary with price under other assumptions.

This glossary of economics is a list of definitions containing terms and concepts used in economics, its sub-disciplines, and related fields.