Equations
Logistic growth equation:
Competitive Lotka–Volterra equations:
A population model is a type of mathematical model that is applied to the study of population dynamics.
Models allow a better understanding of how complex interactions and processes work. Modeling of dynamic interactions in nature can provide a manageable way of understanding how numbers change over time or in relation to each other. Many patterns can be noticed by using population modeling as a tool. [1]
Ecological population modeling is concerned with the changes in parameters such as population size and age distribution within a population. This might be due to interactions with the environment, individuals of their own species, or other species. [2]
Population models are used to determine maximum harvest for agriculturists, to understand the dynamics of biological invasions, and for environmental conservation. Population models are also used to understand the spread of parasites, viruses, and disease. [2]
Another way populations models are useful are when species become endangered. Population models can track the fragile species and work and curb the decline.
Late 18th-century biologists began to develop techniques in population modeling in order to understand the dynamics of growing and shrinking of all populations of living organisms. Thomas Malthus was one of the first to note that populations grew with a geometric pattern while contemplating the fate of humankind. [3] One of the most basic and milestone models of population growth was the logistic model of population growth formulated by Pierre François Verhulst in 1838. The logistic model takes the shape of a sigmoid curve and describes the growth of a population as exponential, followed by a decrease in growth, and bound by a carrying capacity due to environmental pressures. [4]
Population modeling became of particular interest to biologists in the 20th century as pressure on limited means of sustenance due to increasing human populations in parts of Europe were noticed by biologist like Raymond Pearl. In 1921 Pearl invited physicist Alfred J. Lotka to assist him in his lab. Lotka developed paired differential equations that showed the effect of a parasite on its prey. Mathematician Vito Volterra equated the relationship between two species independent from Lotka. Together, Lotka and Volterra formed the Lotka–Volterra model for competition that applies the logistic equation to two species illustrating competition, predation, and parasitism interactions between species. [3] In 1939 contributions to population modeling were given by Patrick Leslie as he began work in biomathematics. Leslie emphasized the importance of constructing a life table in order to understand the effect that key life history strategies played in the dynamics of whole populations. Matrix algebra was used by Leslie in conjunction with life tables to extend the work of Lotka. [5] Matrix models of populations calculate the growth of a population with life history variables. Later, Robert MacArthur and E. O. Wilson characterized island biogeography. The equilibrium model of island biogeography describes the number of species on an island as an equilibrium of immigration and extinction. The logistic population model, the Lotka–Volterra model of community ecology, life table matrix modeling, the equilibrium model of island biogeography and variations thereof are the basis for ecological population modeling today. [6]
Logistic growth equation:
Competitive Lotka–Volterra equations:


Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world.

A logistic function or logistic curve is a common S-shaped curve with the equation
In population ecology and economics, maximum sustainable yield (MSY) is theoretically, the largest yield that can be taken from a species' stock over an indefinite period. Fundamental to the notion of sustainable harvest, the concept of MSY aims to maintain the population size at the point of maximum growth rate by harvesting the individuals that would normally be added to the population, allowing the population to continue to be productive indefinitely. Under the assumption of logistic growth, resource limitation does not constrain individuals' reproductive rates when populations are small, but because there are few individuals, the overall yield is small. At intermediate population densities, also represented by half the carrying capacity, individuals are able to breed to their maximum rate. At this point, called the maximum sustainable yield, there is a surplus of individuals that can be harvested because growth of the population is at its maximum point due to the large number of reproducing individuals. Above this point, density dependent factors increasingly limit breeding until the population reaches carrying capacity. At this point, there are no surplus individuals to be harvested and yield drops to zero. The maximum sustainable yield is usually higher than the optimum sustainable yield and maximum economic yield.
The Lotka–Volterra equations, also known as the Lotka–Volterra predator–prey model, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:

Pierre François Verhulst was a Belgian mathematician and a doctor in number theory from the University of Ghent in 1825. He is best known for the logistic growth model.
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems.

A metapopulation consists of a group of spatially separated populations of the same species which interact at some level. The term metapopulation was coined by Richard Levins in 1969 to describe a model of population dynamics of insect pests in agricultural fields, but the idea has been most broadly applied to species in naturally or artificially fragmented habitats. In Levins' own words, it consists of "a population of populations".
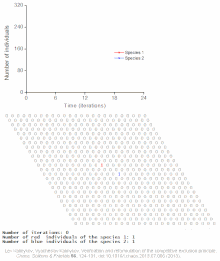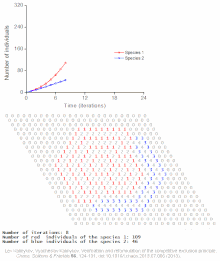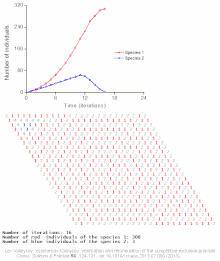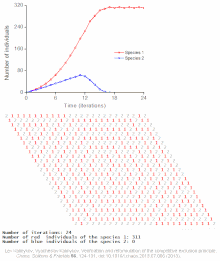
The competitive Lotka–Volterra equations are a simple model of the population dynamics of species competing for some common resource. They can be further generalised to the generalized Lotka–Volterra equation to include trophic interactions.
In ecology, an ecosystem is said to possess ecological stability if it is capable of returning to its equilibrium state after a perturbation or does not experience unexpected large changes in its characteristics across time. Although the terms community stability and ecological stability are sometimes used interchangeably, community stability refers only to the characteristics of communities. It is possible for an ecosystem or a community to be stable in some of their properties and unstable in others. For example, a vegetation community in response to a drought might conserve biomass but lose biodiversity.
The paradox of enrichment is a term from population ecology coined by Michael Rosenzweig in 1971. He described an effect in six predator–prey models where increasing the food available to the prey caused the predator's population to destabilize. A common example is that if the food supply of a prey such as a rabbit is overabundant, its population will grow unbounded and cause the predator population to grow unsustainably large. That may result in a crash in the population of the predators and possibly lead to local eradication or even species extinction.

A fishery is an area with an associated fish or aquatic population which is harvested for its commercial or recreational value. Fisheries can be wild or farmed. Population dynamics describes the ways in which a given population grows and shrinks over time, as controlled by birth, death, and migration. It is the basis for understanding changing fishery patterns and issues such as habitat destruction, predation and optimal harvesting rates. The population dynamics of fisheries is used by fisheries scientists to determine sustainable yields.
In mathematical biology, the community matrix is the linearization of a generalized Lotka–Volterra equation at an equilibrium point. The eigenvalues of the community matrix determine the stability of the equilibrium point.
Limiting similarity is a concept in theoretical ecology and community ecology that proposes the existence of a maximum level of niche overlap between two given species that will allow continued coexistence.
The paradox of the pesticides is a paradox that states that applying pesticide to a pest may end up increasing the abundance of the pest if the pesticide upsets natural predator–prey dynamics in the ecosystem.
In the study of age-structured population growth, probably one of the most important equations is the Euler–Lotka equation. Based on the age demographic of females in the population and female births, this equation allows for an estimation of how a population is growing.
The generalized Lotka–Volterra equations are a set of equations which are more general than either the competitive or predator–prey examples of Lotka–Volterra types. They can be used to model direct competition and trophic relationships between an arbitrary number of species. Their dynamics can be analysed analytically to some extent. This makes them useful as a theoretical tool for modeling food webs. However, they lack features of other ecological models such as predator preference and nonlinear functional responses, and they cannot be used to model mutualism without allowing indefinite population growth.
The Arditi–Ginzburg equations describe ratio-dependent predator–prey dynamics. Where N is the population of a prey species and P that of a predator, the population dynamics are described by the following two equations:

Heteroclinic channels are ensembles of trajectories that can connect saddle equilibrium points in phase space. Dynamical systems and their associated phase spaces can be used to describe natural phenomena in mathematical terms; heteroclinic channels, and the cycles that they produce, are features in phase space that can be designed to occupy specific locations in that space. Heteroclinic channels move trajectories from one equilibrium point to another. More formally, a heteroclinic channel is a region in phase space in which nearby trajectories are drawn closer and closer to one unique limiting trajectory, the heteroclinic orbit. Equilibria connected by heteroclinic trajectories form heteroclinic cycles and cycles can be connected to form heteroclinic networks. Heteroclinic cycles and networks naturally appear in a number of applications, such as fluid dynamics, population dynamics, and neural dynamics. In addition, dynamical systems are often used as methods for robotic control. In particular, for robotic control, the equilibrium points can correspond to robotic states, and the heteroclinic channels can provide smooth methods for switching from state to state.
In theoretical ecology and nonlinear dynamics, consumer-resource models (CRMs) are a class of ecological models in which a community of consumer species compete for a common pool of resources. Instead of species interacting directly, all species-species interactions are mediated through resource dynamics. Consumer-resource models have served as fundamental tools in the quantitative development of theories of niche construction, coexistence, and biological diversity. These models can be interpreted as a quantitative description of a single trophic level.
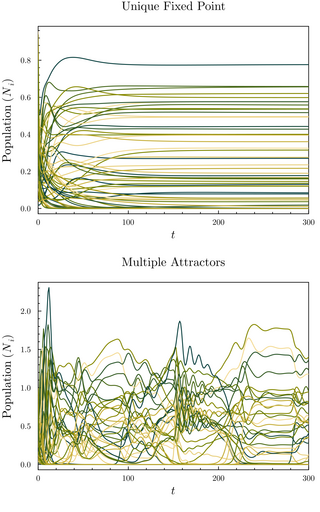
The random generalized Lotka–Volterra model (rGLV) is an ecological model and random set of coupled ordinary differential equations where the parameters of the generalized Lotka–Volterra equation are sampled from a probability distribution, analogously to quenched disorder. The rGLV models dynamics of a community of species in which each species' abundance grows towards a carrying capacity but is depleted due to competition from the presence of other species. It is often analyzed in the many-species limit using tools from statistical physics, in particular from spin glass theory.