Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference." An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships." Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today.

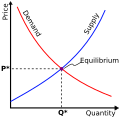
Microeconomics is a branch of economics that studies the behavior of individuals and firms in making decisions regarding the allocation of scarce resources and the interactions among these individuals and firms. Microeconomics focuses on the study of individual markets, sectors, or industries as opposed to the economy as a whole, which is studied in macroeconomics.

Macroeconomics is a branch of economics that deals with the performance, structure, behavior, and decision-making of an economy as a whole. This includes national, regional, and global economies. Macroeconomists study topics such as output/GDP and national income, unemployment, price indices and inflation, consumption, saving, investment, energy, international trade, and international finance.
A mathematical model is an abstract description of a concrete system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in applied mathematics and in the natural sciences and engineering disciplines, as well as in non-physical systems such as the social sciences. It can also be taught as a subject in its own right.
Rational expectations is an economic theory that seeks to infer the macroeconomic consequences of individuals' decisions based on all available knowledge. It assumes that individuals' actions are based on the best available economic theory and information, and concludes that government policies cannot succeed by assuming widespread systematic error by individuals.

This aims to be a complete article list of economics topics:

The Lucas critique argues that it is naïve to try to predict the effects of a change in economic policy entirely on the basis of relationships observed in historical data, especially highly aggregated historical data. More formally, it states that the decision rules of Keynesian models—such as the consumption function—cannot be considered as structural in the sense of being invariant with respect to changes in government policy variables. It was named after American economist Robert Lucas's work on macroeconomic policymaking.
Sensitivity analysis is the study of how the uncertainty in the output of a mathematical model or system can be divided and allocated to different sources of uncertainty in its inputs. This involves estimating sensitivity indices that quantify the influence of an input or group of inputs on the output. A related practice is uncertainty analysis, which has a greater focus on uncertainty quantification and propagation of uncertainty; ideally, uncertainty and sensitivity analysis should be run in tandem.
A macroeconomic model is an analytical tool designed to describe the operation of the problems of economy of a country or a region. These models are usually designed to examine the comparative statics and dynamics of aggregate quantities such as the total amount of goods and services produced, total income earned, the level of employment of productive resources, and the level of prices.
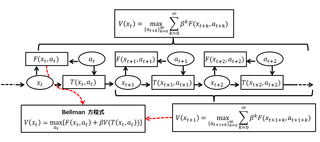
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.
Econometric models are statistical models used in econometrics. An econometric model specifies the statistical relationship that is believed to hold between the various economic quantities pertaining to a particular economic phenomenon. An econometric model can be derived from a deterministic economic model by allowing for uncertainty, or from an economic model which itself is stochastic. However, it is also possible to use econometric models that are not tied to any specific economic theory.

Articles in economics journals are usually classified according to JEL classification codes, which derive from the Journal of Economic Literature. The JEL is published quarterly by the American Economic Association (AEA) and contains survey articles and information on recently published books and dissertations. The AEA maintains EconLit, a searchable data base of citations for articles, books, reviews, dissertations, and working papers classified by JEL codes for the years from 1969. A recent addition to EconLit is indexing of economics journal articles from 1886 to 1968 parallel to the print series Index of Economic Articles.

Lars Peter Hansen is an American economist. He is the David Rockefeller Distinguished Service Professor in Economics, Statistics, and the Booth School of Business, at the University of Chicago and a 2013 recipient of the Nobel Memorial Prize in Economics.
Economics education or economic education is a field within economics that focuses on two main themes:
Qualitative economics is the representation and analysis of information about the direction of change in some economic variable(s) as related to change of some other economic variable(s). For the non-zero case, what makes the change qualitative is that its direction but not its magnitude is specified.

Dynamic stochastic general equilibrium modeling is a macroeconomic method which is often employed by monetary and fiscal authorities for policy analysis, explaining historical time-series data, as well as future forecasting purposes. DSGE econometric modelling applies general equilibrium theory and microeconomic principles in a tractable manner to postulate economic phenomena, such as economic growth and business cycles, as well as policy effects and market shocks.

Mathematical economics is the application of mathematical methods to represent theories and analyze problems in economics. Often, these applied methods are beyond simple geometry, and may include differential and integral calculus, difference and differential equations, matrix algebra, mathematical programming, or other computational methods. Proponents of this approach claim that it allows the formulation of theoretical relationships with rigor, generality, and simplicity.
The methodology of econometrics is the study of the range of differing approaches to undertaking econometric analysis.
Real business-cycle theory is a class of new classical macroeconomics models in which business-cycle fluctuations are accounted for by real shocks. Unlike other leading theories of the business cycle, RBC theory sees business cycle fluctuations as the efficient response to exogenous changes in the real economic environment. That is, the level of national output necessarily maximizes expected utility, and governments should therefore concentrate on long-run structural policy changes and not intervene through discretionary fiscal or monetary policy designed to actively smooth out economic short-term fluctuations.
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field.