Dynamic equilibrium

Last updated November 25, 2024

In chemistry, a dynamic equilibrium exists once a reversible reaction occurs. Substances transition between the reactants and products at equal rates, meaning there is no net change. Reactants and products are formed at such a rate that the concentration of neither changes. It is a particular example of a system in a steady state.

In physics, concerning thermodynamics, a closed system is in thermodynamic equilibrium when reactions occur at such rates that the composition of the mixture does not change with time. Reactions do in fact occur, sometimes vigorously, but to such an extent that changes in composition cannot be observed. Equilibrium constants can be expressed in terms of the rate constants for reversible reactions.

Examples

In a new bottle of soda, the concentration of carbon dioxide in the liquid phase has a particular value. If half of the liquid is poured out and the bottle is sealed, carbon dioxide will leave the liquid phase at an ever-decreasing rate, and the partial pressure of carbon dioxide in the gas phase will increase until equilibrium is reached. At that point, due to thermal motion, a molecule of CO₂ may leave the liquid phase, but within a very short time another molecule of CO₂ will pass from the gas to the liquid, and vice versa. At equilibrium, the rate of transfer of CO₂ from the gas to the liquid phase is equal to the rate from liquid to gas. In this case, the equilibrium concentration of CO₂ in the liquid is given by Henry's law, which states that the solubility of a gas in a liquid is directly proportional to the partial pressure of that gas above the liquid.^[1] This relationship is written as

c=KP

where K is a temperature-dependent constant, P is the partial pressure, and c is the concentration of the dissolved gas in the liquid. Thus the partial pressure of CO₂ in the gas has increased until Henry's law is obeyed. The concentration of carbon dioxide in the liquid has decreased and the drink has lost some of its fizz.

Henry's law may be derived by setting the chemical potentials of carbon dioxide in the two phases to be equal to each other. Equality of chemical potential defines chemical equilibrium. Other constants for dynamic equilibrium involving phase changes, include partition coefficient and solubility product. Raoult's law defines the equilibrium vapor pressure of an ideal solution

Dynamic equilibrium can also exist in a single-phase system. A simple example occurs with acid-base equilibrium such as the dissociation of acetic acid, in an aqueous solution.

{\ce {CH3COOH <=> CH3COO- + H+}}

At equilibrium the concentration quotient, K, the acid dissociation constant, is constant (subject to some conditions)

K_{c}=\mathrm {\frac {[CH_{3}CO_{2}^{-}][H^{+}]}{[CH_{3}CO_{2}H]}}

In this case, the forward reaction involves the liberation of some protons from acetic acid molecules and the backward reaction involves the formation of acetic acid molecules when an acetate ion accepts a proton. Equilibrium is attained when the sum of chemical potentials of the species on the left-hand side of the equilibrium expression is equal to the sum of chemical potentials of the species on the right-hand side. At the same time, the rates of forward and backward reactions are equal to each other. Equilibria involving the formation of chemical complexes are also dynamic equilibria and concentrations are governed by the stability constants of complexes.

Dynamic equilibria can also occur in the gas phase as, for example when nitrogen dioxide dimerizes.

{\ce {2NO2 <=> N2O4}}

;

K_{p}=\mathrm {\frac {[N_{2}O_{4}]}{[NO_{2}]^{2}}}

In the gas phase, square brackets indicate partial pressure. Alternatively, the partial pressure of a substance may be written as P(substance).^[2]

Relationship between equilibrium and rate constants

In a simple reaction such as the isomerization:

{\ce {A <=> B}}

there are two reactions to consider, the forward reaction in which the species A is converted into B and the backward reaction in which B is converted into A. If both reactions are elementary reactions, then the rate of reaction is given by^[3]

{\frac {d[{\ce {A}}]}{dt}}=-k_{f}[{\ce {A}}]_{t}+k_{b}[{\ce {B}}]_{t}

where $k f$ is the rate constant for the forward reaction and $k b$ is the rate constant for the backward reaction and the square brackets, $[\dots]$ , denote concentration. If only A is present at the beginning, time $t = 0$ , with a concentration [A]₀, the sum of the two concentrations, [A]_t and [B]_t, at time $t$ , will be equal to [A]₀.

{\frac {d[{\ce {A}}]}{dt}}=-k_{f}[{\ce {A}}]_{t}+k_{b}\left([{\ce {A}}]_{0}-[{\ce {A}}]_{t}\right)

The solution to this differential equation is

[{\ce {A}}]_{t}={\frac {k_{b}+k_{f}e^{-\left(k_{f}+k_{b}\right)t}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}

and is illustrated at the right. As time tends towards infinity, the concentrations [A]_t and [B]_t tend towards constant values. Let $t$ approach infinity, that is, $t \to \infty$ , in the expression above:

[{\ce {A}}]_{\infty }={\frac {k_{b}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}\qquad [{\ce {B}}]_{\infty }={\frac {k_{f}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}

In practice, concentration changes will not be measurable after ${\textstyle t\gtrapprox {\frac {10}{k_{f}+k_{b}}}.}$ Since the concentrations do not change thereafter, they are, by definition, equilibrium concentrations. Now, the equilibrium constant for the reaction is defined as

K={\frac {[{\ce {B}}]_{\text{eq}}}{[{\ce {A}}]_{\text{eq}}}}

It follows that the equilibrium constant is numerically equal to the quotient of the rate constants.

K={\frac {{\frac {k_{f}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}}{{\frac {k_{b}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}}}={\frac {k_{f}}{k_{b}}}

In general, there may be more than one forward reaction and more than one backward reaction. Atkins states^[3] that, for a general reaction, the overall equilibrium constant is related to the rate constants of the elementary reactions by

K=\left({\frac {k_{f}}{k_{b}}}\right)_{1}\times \left({\frac {k_{f}}{k_{b}}}\right)_{2}\times \cdots

Related Research Articles

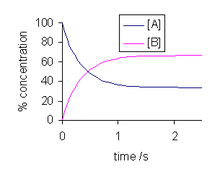
In a chemical reaction, chemical equilibrium is the state in which both the reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium.

Combustion, or burning, is a high-temperature exothermic redox chemical reaction between a fuel and an oxidant, usually atmospheric oxygen, that produces oxidized, often gaseous products, in a mixture termed as smoke. Combustion does not always result in fire, because a flame is only visible when substances undergoing combustion vaporize, but when it does, a flame is a characteristic indicator of the reaction. While activation energy must be supplied to initiate combustion, the heat from a flame may provide enough energy to make the reaction self-sustaining. The study of combustion is known as combustion science.

In a mixture of gases, each constituent gas has a partial pressure which is the notional pressure of that constituent gas as if it alone occupied the entire volume of the original mixture at the same temperature. The total pressure of an ideal gas mixture is the sum of the partial pressures of the gases in the mixture.

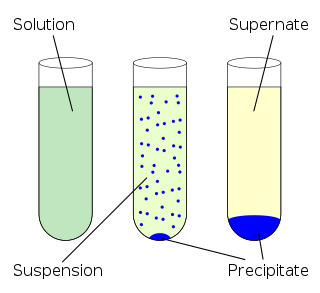
In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.

Solubility equilibrium is a type of dynamic equilibrium that exists when a chemical compound in the solid state is in chemical equilibrium with a solution of that compound. The solid may dissolve unchanged, with dissociation, or with chemical reaction with another constituent of the solution, such as acid or alkali. Each solubility equilibrium is characterized by a temperature-dependent solubility product which functions like an equilibrium constant. Solubility equilibria are important in pharmaceutical, environmental and many other scenarios.

In physical chemistry, Henry's law is a gas law that states that the amount of dissolved gas in a liquid is directly proportional at equilibrium to its partial pressure above the liquid. The proportionality factor is called Henry's law constant. It was formulated by the English chemist William Henry, who studied the topic in the early 19th century. In simple words, we can say that the partial pressure of a gas in vapour phase is directly proportional to the mole fraction of a gas in solution.

<span class="mw-page-title-main">Reaction rate</span> Speed at which a chemical reaction takes place

The reaction rate or rate of reaction is the speed at which a chemical reaction takes place, defined as proportional to the increase in the concentration of a product per unit time and to the decrease in the concentration of a reactant per unit time. Reaction rates can vary dramatically. For example, the oxidative rusting of iron under Earth's atmosphere is a slow reaction that can take many years, but the combustion of cellulose in a fire is a reaction that takes place in fractions of a second. For most reactions, the rate decreases as the reaction proceeds. A reaction's rate can be determined by measuring the changes in concentration over time.

In chemistry, the law of mass action is the proposition that the rate of a chemical reaction is directly proportional to the product of the activities or concentrations of the reactants. It explains and predicts behaviors of solutions in dynamic equilibrium. Specifically, it implies that for a chemical reaction mixture that is in equilibrium, the ratio between the concentration of reactants and products is constant.

The self-ionization of water (also autoionization of water, autoprotolysis of water, autodissociation of water, or simply dissociation of water) is an ionization reaction in pure water or in an aqueous solution, in which a water molecule, H₂O, deprotonates (loses the nucleus of one of its hydrogen atoms) to become a hydroxide ion, OH⁻. The hydrogen nucleus, H⁺, immediately protonates another water molecule to form a hydronium cation, H₃O⁺. It is an example of autoprotolysis, and exemplifies the amphoteric nature of water.

Chemical kinetics, also known as reaction kinetics, is the branch of physical chemistry that is concerned with understanding the rates of chemical reactions. It is different from chemical thermodynamics, which deals with the direction in which a reaction occurs but in itself tells nothing about its rate. Chemical kinetics includes investigations of how experimental conditions influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition states, as well as the construction of mathematical models that also can describe the characteristics of a chemical reaction.

A reversible reaction is a reaction in which the conversion of reactants to products and the conversion of products to reactants occur simultaneously.

The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.

In thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of chemical equilibrium. It is equal to the pressure of an ideal gas which has the same temperature and molar Gibbs free energy as the real gas.

In chemistry, the rate equation is an empirical differential mathematical expression for the reaction rate of a given reaction in terms of concentrations of chemical species and constant parameters only. For many reactions, the initial rate is given by a power law such as

The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes. It states that at equilibrium, each elementary process is in equilibrium with its reverse process.

In electrochemistry, and more generally in solution chemistry, a Pourbaix diagram, also known as a potential/pH diagram, E_H–pH diagram or a pE/pH diagram, is a plot of possible thermodynamically stable phases of an aqueous electrochemical system. Boundaries (50 %/50 %) between the predominant chemical species are represented by lines. As such a Pourbaix diagram can be read much like a standard phase diagram with a different set of axes. Similarly to phase diagrams, they do not allow for reaction rate or kinetic effects. Beside potential and pH, the equilibrium concentrations are also dependent upon, e.g., temperature, pressure, and concentration. Pourbaix diagrams are commonly given at room temperature, atmospheric pressure, and molar concentrations of 10⁻⁶ and changing any of these parameters will yield a different diagram.

In biochemistry, receptor–ligand kinetics is a branch of chemical kinetics in which the kinetic species are defined by different non-covalent bindings and/or conformations of the molecules involved, which are denoted as receptor(s) and ligand(s). Receptor–ligand binding kinetics also involves the on- and off-rates of binding.

In electrochemistry, the Butler–Volmer equation, also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:

The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressure; i.e., at these conditions the adsorbate's partial pressure $is related to its volume V adsorbed onto a solid adsorbent. The adsorbent, as indicated in the figure, is assumed to be an ideal solid surface composed of a series of distinct sites capable of binding the adsorbate. The adsorbate binding is treated as a chemical reaction between the adsorbate gaseous molecule and an empty sorption site S . This reaction yields an adsorbed species with an associated equilibrium constant :$

Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordinate is zero. This principle, applied to mixtures at equilibrium provides a definition of an equilibrium constant. Applications include acid–base, host–guest, metal–complex, solubility, partition, chromatography and redox equilibria.

References

Atkins, P.W.; de Paula, J. (2006). Physical Chemistry (8th. ed.). Oxford University Press. ISBN 0-19-870072-5.

↑ Atkins, Section 5.3
↑ Denbeigh, K (1981). The principles of chemical equilibrium (4th. ed.). Cambridge, U.K.: Cambridge University Press. ISBN 0-521-28150-4.
1 2 Atkins, Section 22.4

External links

Dynamic Equilibrium Example - Wolfram Demonstrations Project

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Atkins, Section 5.3

[2] Denbeigh, K (1981). The principles of chemical equilibrium (4th. ed.). Cambridge, U.K.: Cambridge University Press. ISBN 0-521-28150-4.

[auto-3] 1 2 Atkins, Section 22.4

[1]

[2]

[3]

v t e Chemical equilibria
Concepts	Chemical stability Chelation Dynamic equilibrium Equilibrium chemistry Equilibrium stage Free energy Gibbs Helmholtz Le Chatelier's principle Phase separation Reversible reaction Thermodynamic equilibrium
Models	Equilibrium constant determination Phase diagram Predominance diagram Phase rule Reaction quotient Thermodynamic activity
Applications	Buffer solution Equilibrium unfolding Liquid–liquid extraction
Specific equilibria	Acid dissociation Hammett acidity function Binding constant Binding selectivity Coordination complexes Macrocyclic effect Dissociation constant Hydrolysis Self-ionization of water Partition Distribution coefficient Solubility Common-ion effect Vapor–liquid Henry's law