In a chemical reaction, chemical equilibrium is the state in which both the reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium.
An acid dissociation constant, Ka, is a quantitative measure of the strength of an acid in solution. It is the equilibrium constant for a chemical reaction

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.
In electrochemistry, the Nernst equation is an equation that relates the reduction potential of a reaction to the standard electrode potential, temperature, and activities of the chemical species undergoing reduction and oxidation. It was named after Walther Nernst, a German physical chemist who formulated the equation.
Circular dichroism (CD) is dichroism involving circularly polarized light, i.e., the differential absorption of left- and right-handed light. Left-hand circular (LHC) and right-hand circular (RHC) polarized light represent two possible spin angular momentum states for a photon, and so circular dichroism is also referred to as dichroism for spin angular momentum. This phenomenon was discovered by Jean-Baptiste Biot, Augustin Fresnel, and Aimé Cotton in the first half of the 19th century. Circular dichroism and circular birefringence are manifestations of optical activity. It is exhibited in the absorption bands of optically active chiral molecules. CD spectroscopy has a wide range of applications in many different fields. Most notably, UV CD is used to investigate the secondary structure of proteins. UV/Vis CD is used to investigate charge-transfer transitions. Near-infrared CD is used to investigate geometric and electronic structure by probing metal d→d transitions. Vibrational circular dichroism, which uses light from the infrared energy region, is used for structural studies of small organic molecules, and most recently proteins and DNA.

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum reversible work that may be performed by a thermodynamic system at a constant temperature and pressure. The Gibbs free energy (, measured in joules in SI) is the maximum amount of non-expansion work that can be extracted from a thermodynamically closed system. This maximum can be attained only in a completely reversible process. When a system transforms reversibly from an initial state to a final state, the decrease in Gibbs free energy equals the work done by the system to its surroundings, minus the work of the pressure forces.
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.

In supramolecular chemistry, host–guest chemistry describes complexes that are composed of two or more molecules or ions that are held together in unique structural relationships by forces other than those of full covalent bonds. Host–guest chemistry encompasses the idea of molecular recognition and interactions through non-covalent bonding. Non-covalent bonding is critical in maintaining the 3D structure of large molecules, such as proteins and is involved in many biological processes in which large molecules bind specifically but transiently to one another.
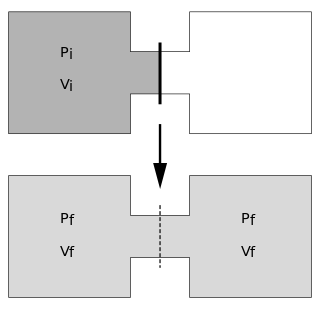
The Joule expansion is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container, with the other side of the container being evacuated. The partition between the two parts of the container is then opened, and the gas fills the whole container.

In electrochemistry, and more generally in solution chemistry, a Pourbaix diagram, also known as a potential/pH diagram, EH–pH diagram or a pE/pH diagram, is a plot of possible thermodynamically stable phases of an aqueous electrochemical system. Boundaries (50 %/50 %) between the predominant chemical species are represented by lines. As such a Pourbaix diagram can be read much like a standard phase diagram with a different set of axes. Similarly to phase diagrams, they do not allow for reaction rate or kinetic effects. Beside potential and pH, the equilibrium concentrations are also dependent upon, e.g., temperature, pressure, and concentration. Pourbaix diagrams are commonly given at room temperature, atmospheric pressure, and molar concentrations of 10−6 and changing any of these parameters will yield a different diagram.
The Van 't Hoff equation relates the change in the equilibrium constant, Keq, of a chemical reaction to the change in temperature, T, given the standard enthalpy change, ΔrH⊖, for the process. It was proposed by Dutch chemist Jacobus Henricus van 't Hoff in 1884 in his book Études de dynamique chimique.
Phi value analysis, analysis, or -value analysis is an experimental protein engineering technique for studying the structure of the folding transition state of small protein domains that fold in a two-state manner. The structure of the folding transition state is hard to find using methods such as protein NMR or X-ray crystallography because folding transitions states are mobile and partly unstructured by definition. In -value analysis, the folding kinetics and conformational folding stability of the wild-type protein are compared with those of point mutants to find phi values. These measure the mutant residue's energetic contribution to the folding transition state, which reveals the degree of native structure around the mutated residue in the transition state, by accounting for the relative free energies of the unfolded state, the folded state, and the transition state for the wild-type and mutant proteins.

This article is a summary of common equations and quantities in thermodynamics.

Transition state theory (TST) explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.
Nucleic acid thermodynamics is the study of how temperature affects the nucleic acid structure of double-stranded DNA (dsDNA). The melting temperature (Tm) is defined as the temperature at which half of the DNA strands are in the random coil or single-stranded (ssDNA) state. Tm depends on the length of the DNA molecule and its specific nucleotide sequence. DNA, when in a state where its two strands are dissociated, is referred to as having been denatured by the high temperature.
Equilibrium constants are determined in order to quantify chemical equilibria. When an equilibrium constant K is expressed as a concentration quotient,

The Gaussian network model (GNM) is a representation of a biological macromolecule as an elastic mass-and-spring network to study, understand, and characterize the mechanical aspects of its long-time large-scale dynamics. The model has a wide range of applications from small proteins such as enzymes composed of a single domain, to large macromolecular assemblies such as a ribosome or a viral capsid. Protein domain dynamics plays key roles in a multitude of molecular recognition and cell signalling processes. Protein domains, connected by intrinsically disordered flexible linker domains, induce long-range allostery via protein domain dynamics. The resultant dynamic modes cannot be generally predicted from static structures of either the entire protein or individual domains.

The non-random two-liquid model is an activity coefficient model that correlates the activity coefficients of a compound with its mole fractions in the liquid phase concerned. It is frequently applied in the field of chemical engineering to calculate phase equilibria. The concept of NRTL is based on the hypothesis of Wilson that the local concentration around a molecule is different from the bulk concentration. This difference is due to a difference between the interaction energy of the central molecule with the molecules of its own kind and that with the molecules of the other kind . The energy difference also introduces a non-randomness at the local molecular level. The NRTL model belongs to the so-called local-composition models. Other models of this type are the Wilson model, the UNIQUAC model, and the group contribution model UNIFAC. These local-composition models are not thermodynamically consistent for a one-fluid model for a real mixture due to the assumption that the local composition around molecule i is independent of the local composition around molecule j. This assumption is not true, as was shown by Flemr in 1976. However, they are consistent if a hypothetical two-liquid model is used.

The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressure i.e at these conditions the adsorbate's partial pressure, , is related to the volume of it, V, adsorbed onto a solid adsorbent. The adsorbent, as indicated in the figure, is assumed to be an ideal solid surface composed of a series of distinct sites capable of binding the adsorbate. The adsorbate binding is treated as a chemical reaction between the adsorbate gaseous molecule and an empty sorption site, S. This reaction yields an adsorbed species with an associated equilibrium constant :
Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordinate is zero. This principle, applied to mixtures at equilibrium provides a definition of an equilibrium constant. Applications include acid–base, host–guest, metal–complex, solubility, partition, chromatography and redox equilibria.





























































