
In biochemistry, denaturation is a process in which proteins or nucleic acids lose the quaternary structure, tertiary structure, and secondary structure which is present in their native state, by application of some external stress or compound such as a strong acid or base, a concentrated inorganic salt, an organic solvent, agitation and radiation or heat. If proteins in a living cell are denatured, this results in disruption of cell activity and possibly cell death. Protein denaturation is also a consequence of cell death. Denatured proteins can exhibit a wide range of characteristics, from conformational change and loss of solubility to aggregation due to the exposure of hydrophobic groups. The loss of solubility as a result of denaturation is called coagulation. Denatured proteins lose their 3D structure and therefore cannot function.
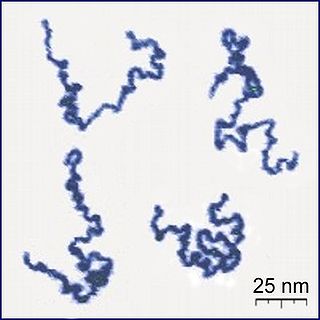
A polymer is a substance or material consisting of very large molecules called macromolecules, composed of many repeating subunits. Due to their broad spectrum of properties, both synthetic and natural polymers play essential and ubiquitous roles in everyday life. Polymers range from familiar synthetic plastics such as polystyrene to natural biopolymers such as DNA and proteins that are fundamental to biological structure and function. Polymers, both natural and synthetic, are created via polymerization of many small molecules, known as monomers. Their consequently large molecular mass, relative to small molecule compounds, produces unique physical properties including toughness, high elasticity, viscoelasticity, and a tendency to form amorphous and semicrystalline structures rather than crystals.

Protein secondary structure is the local spatial conformation of the polypeptide backbone excluding the side chains. The two most common secondary structural elements are alpha helices and beta sheets, though beta turns and omega loops occur as well. Secondary structure elements typically spontaneously form as an intermediate before the protein folds into its three dimensional tertiary structure.

Polyacrylamide gel electrophoresis (PAGE) is a technique widely used in biochemistry, forensic chemistry, genetics, molecular biology and biotechnology to separate biological macromolecules, usually proteins or nucleic acids, according to their electrophoretic mobility. Electrophoretic mobility is a function of the length, conformation, and charge of the molecule. Polyacrylamide gel electrophoresis is a powerful tool used to analyze RNA samples. When polyacrylamide gel is denatured after electrophoresis, it provides information on the sample composition of the RNA species.
In molecular biology, the term molten globule (MG) refers to protein states that are more or less compact, but are lacking the specific tight packing of amino acid residues which creates the solid state-like tertiary structure of completely folded proteins.

Polymer physics is the field of physics that studies polymers, their fluctuations, mechanical properties, as well as the kinetics of reactions involving degradation and polymerisation of polymers and monomers respectively.
Polymer chemistry is a sub-discipline of chemistry that focuses on the structures of chemicals, chemical synthesis, and chemical and physical properties of polymers and macromolecules. The principles and methods used within polymer chemistry are also applicable through a wide range of other chemistry sub-disciplines like organic chemistry, analytical chemistry, and physical chemistry. Many materials have polymeric structures, from fully inorganic metals and ceramics to DNA and other biological molecules. However, polymer chemistry is typically related to synthetic and organic compositions. Synthetic polymers are ubiquitous in commercial materials and products in everyday use, such as plastics, and rubbers, and are major components of composite materials. Polymer chemistry can also be included in the broader fields of polymer science or even nanotechnology, both of which can be described as encompassing polymer physics and polymer engineering.

Protein structure is the three-dimensional arrangement of atoms in an amino acid-chain molecule. Proteins are polymers – specifically polypeptides – formed from sequences of amino acids, which are the monomers of the polymer. A single amino acid monomer may also be called a residue, which indicates a repeating unit of a polymer. Proteins form by amino acids undergoing condensation reactions, in which the amino acids lose one water molecule per reaction in order to attach to one another with a peptide bond. By convention, a chain under 30 amino acids is often identified as a peptide, rather than a protein. To be able to perform their biological function, proteins fold into one or more specific spatial conformations driven by a number of non-covalent interactions, such as hydrogen bonding, ionic interactions, Van der Waals forces, and hydrophobic packing. To understand the functions of proteins at a molecular level, it is often necessary to determine their three-dimensional structure. This is the topic of the scientific field of structural biology, which employs techniques such as X-ray crystallography, NMR spectroscopy, cryo-electron microscopy (cryo-EM) and dual polarisation interferometry, to determine the structure of proteins.
An ideal chain is the simplest model in polymer chemistry to describe polymers, such as nucleic acids and proteins. It assumes that the monomers in a polymer are located at the steps of a hypothetical random walker that does not remember its previous steps. By neglecting interactions among monomers, this model assumes that two monomers can occupy the same location. Although it is simple, its generality gives insight about the physics of polymers.
The worm-like chain (WLC) model in polymer physics is used to describe the behavior of polymers that are semi-flexible: fairly stiff with successive segments pointing in roughly the same direction, and with persistence length within a few orders of magnitude of the polymer length. The WLC model is the continuous version of the Kratky–Porod model.
In statistical mechanics, the Zimm–Bragg model is a helix-coil transition model that describes helix-coil transitions of macromolecules, usually polymer chains. Most models provide a reasonable approximation of the fractional helicity of a given polypeptide; the Zimm–Bragg model differs by incorporating the ease of propagation (self-replication) with respect to nucleation. It is named for co-discoverers Bruno H. Zimm and J. K. Bragg.
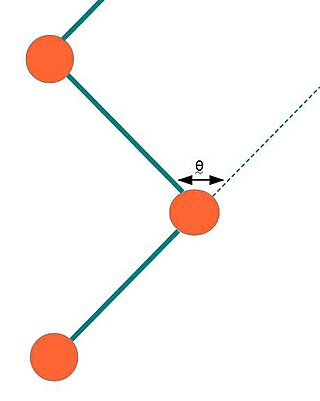
The Kuhn length is a theoretical treatment, developed by Werner Kuhn, in which a real polymer chain is considered as a collection of Kuhn segments each with a Kuhn length . Each Kuhn segment can be thought of as if they are freely jointed with each other. Each segment in a freely jointed chain can randomly orient in any direction without the influence of any forces, independent of the directions taken by other segments. Instead of considering a real chain consisting of bonds and with fixed bond angles, torsion angles, and bond lengths, Kuhn considered an equivalent ideal chain with connected segments, now called Kuhn segments, that can orient in any random direction.
In chemical thermodynamics, conformational entropy is the entropy associated with the number of conformations of a molecule. The concept is most commonly applied to biological macromolecules such as proteins and RNA, but also be used for polysaccharides and other molecules. To calculate the conformational entropy, the possible conformations of the molecule may first be discretized into a finite number of states, usually characterized by unique combinations of certain structural parameters, each of which has been assigned an energy. In proteins, backbone dihedral angles and side chain rotamers are commonly used as parameters, and in RNA the base pairing pattern may be used. These characteristics are used to define the degrees of freedom. The conformational entropy associated with a particular structure or state, such as an alpha-helix, a folded or an unfolded protein structure, is then dependent on the probability of the occupancy of that structure.
Rubber elasticity refers to a property of crosslinked rubber: it can be stretched by up to a factor of 10 from its original length and, when released, returns very nearly to its original length. This can be repeated many times with no apparent degradation to the rubber. Rubber is a member of a larger class of materials called elastomers and it is difficult to overestimate their economic and technological importance. Elastomers have played a key role in the development of new technologies in the 20th century and make a substantial contribution to the global economy. Rubber elasticity is produced by several complex molecular processes and its explanation requires a knowledge of advanced mathematics, chemistry and statistical physics, particularly the concept of entropy. Entropy may be thought of as a measure of the thermal energy that is stored in a molecule. Common rubbers, such as polybutadiene and polyisoprene, are produced by a process called polymerization. Very long molecules (polymers) are built up sequentially by adding short molecular backbone units through chemical reactions. A rubber polymer follows a random, zigzag path in three dimensions, intermingling with many other rubber molecules. An elastomer is created by the addition of a few percent of a cross linking molecule such as sulfur. When heated, the crosslinking molecule causes a reaction that chemically joins (bonds) two of the rubber molecules together at some point. Because the rubber molecules are so long, each one participates in many crosslinks with many other rubber molecules forming a continuous molecular network. As a rubber band is stretched, some of the network chains are forced to become straight and this causes a decrease in their entropy. It is this decrease in entropy that gives rise to the elastic force in the network chains.
Helix–coil transition models are formalized techniques in statistical mechanics developed to describe conformations of linear polymers in solution. The models are usually but not exclusively applied to polypeptides as a measure of the relative fraction of the molecule in an alpha helix conformation versus turn or random coil. The main attraction in investigating alpha helix formation is that one encounters many of the features of protein folding but in their simplest version. Most of the helix–coil models contain parameters for the likelihood of helix nucleation from a coil region, and helix propagation along the sequence once nucleated; because polypeptides are directional and have distinct N-terminal and C-terminal ends, propagation parameters may differ in each direction.
In polymer science, the Lifson–Roig model is a helix-coil transition model applied to the alpha helix-random coil transition of polypeptides; it is a refinement of the Zimm–Bragg model that recognizes that a polypeptide alpha helix is only stabilized by a hydrogen bond only once three consecutive residues have adopted the helical conformation. To consider three consecutive residues each with two states, the Lifson–Roig model uses a 4x4 transfer matrix instead of the 2x2 transfer matrix of the Zimm–Bragg model, which considers only two consecutive residues. However, the simple nature of the coil state allows this to be reduced to a 3x3 matrix for most applications.
In a polymer solution, a theta solvent is a solvent in which polymer coils act like ideal chains, assuming exactly their random walk coil dimensions. Therefore, the Mark–Houwink equation exponent is in a theta solvent. Thermodynamically, the excess chemical potential of mixing between a polymer and a theta solvent is zero.

Abductin is a naturally occurring elastomeric protein found in the hinge ligament of bivalve mollusks. It is unique as it is the only natural elastomer with compressible elasticity, as compared to resilin, spider silk, and elastin. Its name was proposed from the fact that it functions as the abductor of the valves of bivalve mollusks.

A polymer is a macromolecule, composed of many similar or identical repeated subunits. Polymers are common in, but not limited to, organic media. They range from familiar synthetic plastics to natural biopolymers such as DNA and proteins. Their unique elongated molecular structure produces unique physical properties, including toughness, viscoelasticity, and a tendency to form glasses and semicrystalline structures. The modern concept of polymers as covalently bonded macromolecular structures was proposed in 1920 by Hermann Staudinger. One sub-field in the study of polymers is polymer physics. As a part of soft matter studies, Polymer physics concerns itself with the study of mechanical properties and focuses on the perspective of condensed matter physics.
Polymer scattering experiments are one of the main scientific methods used in chemistry, physics and other sciences to study the characteristics of polymeric systems: solutions, gels, compounds and more. As in most scattering experiments, it involves subjecting a polymeric sample to incident particles, and studying the characteristics of the scattered particles: angular distribution, intensity polarization and so on. This method is quite simple and straightforward, and does not require special manipulations of the samples which may alter their properties, and hence compromise exact results.














