
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations.
In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues. More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectrum. The spectral radius is often denoted by ρ(·).
In mathematics, subadditivity is a property of a function that states, roughly, that evaluating the function for the sum of two elements of the domain always returns something less than or equal to the sum of the function's values at each element. There are numerous examples of subadditive functions in various areas of mathematics, particularly norms and square roots. Additive maps are special cases of subadditive functions.
Time consistency in the context of finance is the property of not having mutually contradictory evaluations of risk at different points in time. This property implies that if investment A is considered riskier than B at some future time, then A will also be considered riskier than B at every prior time.
In mathematics, a Fredholm kernel is a certain type of a kernel on a Banach space, associated with nuclear operators on the Banach space. They are an abstraction of the idea of the Fredholm integral equation and the Fredholm operator, and are one of the objects of study in Fredholm theory. Fredholm kernels are named in honour of Erik Ivar Fredholm. Much of the abstract theory of Fredholm kernels was developed by Alexander Grothendieck and published in 1955.
In mathematics, a π-system on a set is a collection of certain subsets of such that
In the fields of actuarial science and financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a function that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance.
Expected shortfall (ES) is a risk measure—a concept used in the field of financial risk measurement to evaluate the market risk or credit risk of a portfolio. The "expected shortfall at q% level" is the expected return on the portfolio in the worst of cases. ES is an alternative to value at risk that is more sensitive to the shape of the tail of the loss distribution.
In financial mathematics, a risk measure is used to determine the amount of an asset or set of assets to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator. In recent years attention has turned towards convex and coherent risk measurement.
A Spectral risk measure is a risk measure given as a weighted average of outcomes where bad outcomes are, typically, included with larger weights. A spectral risk measure is a function of portfolio returns and outputs the amount of the numeraire to be kept in reserve. A spectral risk measure is always a coherent risk measure, but the converse does not always hold. An advantage of spectral measures is the way in which they can be related to risk aversion, and particularly to a utility function, through the weights given to the possible portfolio returns.
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.
Uncertainty theory is a branch of mathematics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms.
The superhedging price is a coherent risk measure. The superhedging price of a portfolio (A) is equivalent to the smallest amount necessary to be paid for an admissible portfolio (B) at the current time so that at some specified future time the value of B is at least as great as A. In a complete market the superhedging price is equivalent to the price for hedging the initial portfolio.
In financial mathematics, acceptance set is a set of acceptable future net worth which is acceptable to the regulator. It is related to risk measures.
In financial mathematics, a deviation risk measure is a function to quantify financial risk in a different method than a general risk measure. Deviation risk measures generalize the concept of standard deviation.
In quantum mechanics, negativity is a measure of quantum entanglement which is easy to compute. It is a measure deriving from the PPT criterion for separability. It has shown to be an entanglement monotone and hence a proper measure of entanglement.
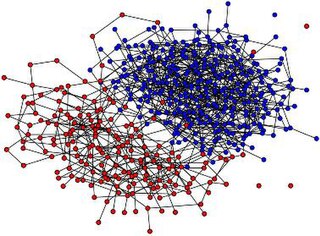
In the mathematical theory of probability, the voter model is an interacting particle system introduced by Richard A. Holley and Thomas M. Liggett in 1975.
The min-entropy, in information theory, is the smallest of the Rényi family of entropies, corresponding to the most conservative way of measuring the unpredictability of a set of outcomes, as the negative logarithm of the probability of the most likely outcome. The various Rényi entropies are all equal for a uniform distribution, but measure the unpredictability of a nonuniform distribution in different ways. The min-entropy is never greater than the ordinary or Shannon entropy and that in turn is never greater than the Hartley or max-entropy, defined as the logarithm of the number of outcomes with nonzero probability.
Regularized least squares (RLS) is a family of methods for solving the least-squares problem while using regularization to further constrain the resulting solution.
In measure and probability theory in mathematics, a convex measure is a probability measure that — loosely put — does not assign more mass to any intermediate set "between" two measurable sets A and B than it does to A or B individually. There are multiple ways in which the comparison between the probabilities of A and B and the intermediate set can be made, leading to multiple definitions of convexity, such as log-concavity, harmonic convexity, and so on. The mathematician Christer Borell was a pioneer of the detailed study of convex measures on locally convex spaces in the 1970s.























