Related Research Articles

A Bézier curve is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape that otherwise has no mathematical representation or whose representation is unknown or too complicated. The Bézier curve is named after French engineer Pierre Bézier (1910–1999), who used it in the 1960s for designing curves for the bodywork of Renault cars. Other uses include the design of computer fonts and animation. Bézier curves can be combined to form a Bézier spline, or generalized to higher dimensions to form Bézier surfaces. The Bézier triangle is a special case of the latter.
Pierre Étienne Bézier was a French engineer and one of the founders of the fields of solid, geometric and physical modelling as well as in the field of representing curves, especially in computer-aided design and manufacturing systems. As an engineer at Renault, he became a leader in the transformation of design and manufacturing, through mathematics and computing tools, into computer-aided design and three-dimensional modeling.

In geometric modelling and in computer graphics, a composite Bézier curve or Bézier spline is a spline made out of Bézier curves that is at least continuous. In other words, a composite Bézier curve is a series of Bézier curves joined end to end where the last point of one curve coincides with the starting point of the next curve. Depending on the application, additional smoothness requirements may be added.

In vector computer graphics, CAD systems, and geographic information systems, geometric primitive is the simplest geometric shape that the system can handle. Sometimes the subroutines that draw the corresponding objects are called "geometric primitives" as well. The most "primitive" primitives are point and straight line segment, which were all that early vector graphics systems had.

The Utah teapot, or the Newell teapot, is one of the standard reference test models in 3D modeling and an in-joke within the computer graphics community. It is a mathematical model of an ordinary Melitta-brand teapot designed by Lieselotte Kantner that appears solid with a nearly rotationally symmetrical body. Using a teapot model is considered the 3D equivalent of a "Hello, World!" program, a way to create an easy 3D scene with a somewhat complex model acting as the basic geometry for a scene with a light setup. Some programming libraries, such as the OpenGL Utility Toolkit, even have functions dedicated to drawing teapots.
Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling. As with Bézier curves, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive and, for many applications, mathematically convenient.

Non-uniform rational basis spline (NURBS) is a mathematical model using basis splines (B-splines) that is commonly used in computer graphics for representing curves and surfaces. It offers great flexibility and precision for handling both analytic and modeled shapes. It is a type of curve modeling, as opposed to polygonal modeling or digital sculpting. NURBS curves are commonly used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE). They are part of numerous industry-wide standards, such as IGES, STEP, ACIS, and PHIGS. Tools for creating and editing NURBS surfaces are found in various 3D graphics, rendering, and animation software packages.
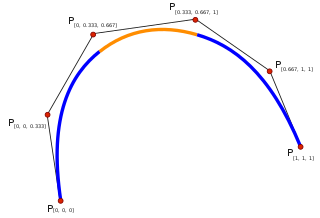
In mathematics, a spline is a function defined piecewise by polynomials. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low degree polynomials, while avoiding Runge's phenomenon for higher degrees.
Paul de Casteljau was a French physicist and mathematician. In 1959, while working at Citroën, he developed an algorithm for evaluating calculations on a certain family of curves, which would later be formalized and popularized by engineer Pierre Bézier, leading to the curves widely known as Bézier curves.
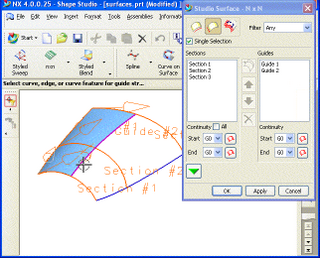
Freeform surface modelling is a technique for engineering freeform surfaces with a CAD or CAID system.
Geometric modeling is a branch of applied mathematics and computational geometry that studies methods and algorithms for the mathematical description of shapes. The shapes studied in geometric modeling are mostly two- or three-dimensional, although many of its tools and principles can be applied to sets of any finite dimension. Today most geometric modeling is done with computers and for computer-based applications. Two-dimensional models are important in computer typography and technical drawing. Three-dimensional models are central to computer-aided design and manufacturing (CAD/CAM), and widely used in many applied technical fields such as civil and mechanical engineering, architecture, geology and medical image processing.

Geometrical design (GD) is a branch of computational geometry. It deals with the construction and representation of free-form curves, surfaces, or volumes and is closely related to geometric modeling. Core problems are curve and surface modelling and representation. GD studies especially the construction and manipulation of curves and surfaces given by a set of points using polynomial, rational, piecewise polynomial, or piecewise rational methods. The most important instruments here are parametric curves and parametric surfaces, such as Bézier curves, spline curves and surfaces. An important non-parametric approach is the level-set method.
In the mathematical fields of numerical analysis and approximation theory, box splines are piecewise polynomial functions of several variables. Box splines are considered as a multivariate generalization of basis splines (B-splines) and are generally used for multivariate approximation/interpolation. Geometrically, a box spline is the shadow (X-ray) of a hypercube projected down to a lower-dimensional space. Box splines and simplex splines are well studied special cases of polyhedral splines which are defined as shadows of general polytopes.
In computer graphics, a T-spline is a mathematical model for defining freeform surfaces. A T-spline surface is a type of surface defined by a network of control points where a row of control points is allowed to terminate without traversing the entire surface. The control net at a terminated row resembles the letter "T".
Solid Modeling Solutions was a software company that specialized in 3D geometry software. SMS was acquired by NVIDIA Corporation of Santa Clara, CA in May 2022 and was dissolved as a separate corporate entity.

The Kahlert School of Computing is a school within the College of Engineering at the University of Utah in Salt Lake City, Utah.
Thomas W. Sederberg is the associate dean of the college of physical and mathematical sciences and professor of Computer Science at Brigham Young University in Provo, Utah. His research involves computer graphics and computer aided design. He helped invent free-form deformation and T-splines.
Nira (Richter) Dyn is an Israeli mathematician who studied geometric modeling, subdivision surfaces, approximation theory, and image compression. She is a professor emeritus of applied mathematics at Tel Aviv University, and has been called a "pioneer and leading researcher in the subdivision community".

Jean J. Pedersen was an American mathematician and author particularly known for her works on the mathematics of paper folding.
Dianne Carol Hansford is an American computer scientist known for her research on Coons patches in computer graphics and for her textbooks on computer-aided geometric design, linear algebra, and the mathematics behind scientific visualization. She is a lecturer at Arizona State University in the School of Computing and Augmented Intelligence, and the cofounder of a startup based on her research, 3D Compression Technologies.
References
- 1 2 Richard Riesenfeld and Elaine Cohen, the 2009 Pierre Bézier Award Recipients, Solid Modeling Association, retrieved 2018-10-27
- ↑ "Elaine Cohen", Faculty profile, University of Utah, retrieved 2018-10-27
- ↑ Education, University of Utah, retrieved 2018-10-27
- ↑ Elaine Cohen at the Mathematics Genealogy Project
- 1 2 "YWCA to honor 6 Utah women: Award recipients are hailed for excellence, beating challenges", Deseret News , September 11, 2005, archived from the original on October 28, 2018
- ↑ Reviews of Geometric Modeling with Splines:
- Walker, Marshall (2002), Mathematical Reviews, MR 1845683
{{citation}}: CS1 maint: untitled periodical (link) - Bletzinger, K.-U. (December 2002), Structural and Multidisciplinary Optimization, 24 (6): 464–465, doi:10.1007/s00158-002-0260-9, S2CID 120598791
{{citation}}: CS1 maint: untitled periodical (link) - Bultheel, A. (2003), "Review", Bulletin of the Belgian Mathematical Society, 10 (1): 159
- Peters, J (October 2003), "Splines with pictures and proofs", Computer-Aided Design, 35 (12): 1144, doi:10.1016/s0010-4485(03)00096-4
- Walker, Marshall (2002), Mathematical Reviews, MR 1845683
- ↑ Piper, Matthew (December 5, 2016), "Whatever happened to ... the ubiquitous digital 'Utah teapot'?", Salt Lake Tribune