
Young's modulus, the Young modulus, or the modulus of elasticity in tension or compression, is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied lengthwise. It quantifies the relationship between tensile/compressive stress and axial strain in the linear elastic region of a material and is determined using the formula:
In physics and materials science, elasticity is the ability of a body to resist a distorting influence and to return to its original size and shape when that influence or force is removed. Solid objects will deform when adequate loads are applied to them; if the material is elastic, the object will return to its initial shape and size after removal. This is in contrast to plasticity, in which the object fails to do so and instead remains in its deformed state.
The field of strength of materials typically refers to various methods of calculating the stresses and strains in structural members, such as beams, columns, and shafts. The methods employed to predict the response of a structure under loading and its susceptibility to various failure modes takes into account the properties of the materials such as its yield strength, ultimate strength, Young's modulus, and Poisson's ratio. In addition, the mechanical element's macroscopic properties such as its length, width, thickness, boundary constraints and abrupt changes in geometry such as holes are considered.
Structural analysis is a branch of solid mechanics which uses simplified models for solids like bars, beams and shells for engineering decision making. Its main objective is to determine the effect of loads on the physical structures and their components. In contrast to theory of elasticity, the models used in structure analysis are often differential equations in one spatial variable. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, aircraft and ships. Structural analysis uses ideas from applied mechanics, materials science and applied mathematics to compute a structure's deformations, internal forces, stresses, support reactions, velocity, accelerations, and stability. The results of the analysis are used to verify a structure's fitness for use, often precluding physical tests. Structural analysis is thus a key part of the engineering design of structures.
Solid mechanics is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents.
Stress–strain analysis is an engineering discipline that uses many methods to determine the stresses and strains in materials and structures subjected to forces. In continuum mechanics, stress is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material.

A beam is a structural element that primarily resists loads applied laterally to the beam's axis. Its mode of deflection is primarily by bending. The loads applied to the beam result in reaction forces at the beam's support points. The total effect of all the forces acting on the beam is to produce shear forces and bending moments within the beams, that in turn induce internal stresses, strains and deflections of the beam. Beams are characterized by their manner of support, profile, equilibrium conditions, length, and their material.

In structural engineering, buckling is the sudden change in shape (deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear. If a structure is subjected to a gradually increasing load, when the load reaches a critical level, a member may suddenly change shape and the structure and component is said to have buckled. Euler's critical load and Johnson's parabolic formula are used to determine the buckling stress of a column.
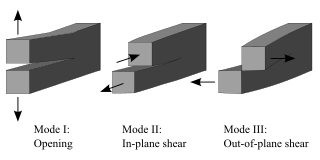
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.

Photoelasticity describes changes in the optical properties of a material under mechanical deformation. It is a property of all dielectric media and is often used to experimentally determine the stress distribution in a material, where it gives a picture of stress distributions around discontinuities in materials. Photoelastic experiments are an important tool for determining critical stress points in a material, and are used for determining stress concentration in irregular geometries.
A mechanician is an engineer or a scientist working in the field of mechanics, or in a related or sub-field: engineering or computational mechanics, applied mechanics, geomechanics, biomechanics, and mechanics of materials. Names other than mechanician have been used occasionally, such as mechaniker and mechanicist.
Micromechanics is the analysis of composite or heterogeneous materials on the level of the individual constituents that constitute these materials.
This is an alphabetical list of articles pertaining specifically to structural engineering. For a broad overview of engineering, please see List of engineering topics. For biographies please see List of engineers.

A shear band is a narrow zone of intense shearing strain, usually of plastic nature, developing during severe deformation of ductile materials. As an example, a soil specimen is shown in Fig. 1, after an axialsymmetric compression test. Initially the sample was cylindrical in shape and, since symmetry was tried to be preserved during the test, the cylindrical shape was maintained for a while during the test and the deformation was homogeneous, but at extreme loading two X-shaped shear bands had formed and the subsequent deformation was strongly localized.

In fluid dynamics, hydrodynamic stability is the field which analyses the stability and the onset of instability of fluid flows. The study of hydrodynamic stability aims to find out if a given flow is stable or unstable, and if so, how these instabilities will cause the development of turbulence. The foundations of hydrodynamic stability, both theoretical and experimental, were laid most notably by Helmholtz, Kelvin, Rayleigh and Reynolds during the nineteenth century. These foundations have given many useful tools to study hydrodynamic stability. These include Reynolds number, the Euler equations, and the Navier–Stokes equations. When studying flow stability it is useful to understand more simplistic systems, e.g. incompressible and inviscid fluids which can then be developed further onto more complex flows. Since the 1980s, more computational methods are being used to model and analyse the more complex flows.

João Arménio Correia Martins was born on November 11, 1951, at the southern town of Olhão in Portugal. He attended high school at the Liceu Nacional de Faro which he completed in 1969. Afterwards João Martins moved to Lisbon where he was graduate student of Civil Engineering at Instituto Superior Técnico (IST) until 1976. He was a research assistant and assistant instructor at IST until 1981. Subsequently, he entered the graduate school in the College of Engineering, Department of Aerospace Engineering and Engineering Mechanics of The University of Texas at Austin, USA. There he obtained a MSc in 1983 with a thesis titled A Numerical Analysis of a Class of Problems in Elastodynamics with Friction Effects and a PhD in 1986 with a thesis titled Dynamic Frictional Contact Problems Involving Metallic Bodies, both supervised by Prof. John Tinsley Oden. He returned to Portugal in 1986 and became assistant professor at IST. In 1989 he became associate professor and in 1996 he earned the academic degree of “agregado” from Universidade Técnica de Lisboa. Later, in 2005, he became full professor in the Department of Civil Engineering and Architecture of IST.
A rigid line inclusion, also called stiffener, is a mathematical model used in solid mechanics to describe a narrow hard phase, dispersed within a matrix material. This inclusion is idealised as an infinitely rigid and thin reinforcement, so that it represents a sort of ‘inverse’ crack, from which the nomenclature ‘anticrack’ derives.
Compaction of ceramic powders is a forming technique for ceramics in which granular ceramic materials are made cohesive through mechanical densification, either by hot or cold pressing. The resulting green part must later be sintered in a kiln. The compaction process permits an efficient production of parts to close tolerances with low drying shrinkage. It can be used for parts ranging widely in size and shape, and for both technical and nontechnical ceramics.
Raymond William Ogden is a British applied mathematician. He is the George Sinclair Professor of Mathematics at the Department of Mathematics and Statistics of the University of Glasgow.

Alain Goriely is a Belgian mathematician, currently holding the statutory professorship (chair) of mathematical modelling at the University of Oxford, Mathematical Institute. He is director of the Oxford Centre for Industrial Mathematics (OCIAM), of the International Brain and Mechanics Lab (IBMTL) and Professorial Fellow at St Catherine's College, Oxford. At the Mathematical Institute, he was the director of external relations and public engagement, from 2013 until 2022, initiating the Oxford Mathematics series of public lectures. In 2022, he was elected to the Royal Society.










