Empirical statistical laws

Last updated

An empirical statistical law or (in popular terminology) a law of statistics represents a type of behaviour that has been found across a number of datasets and, indeed, across a range of types of data sets. [1] Many of these observances have been formulated and proved as statistical or probabilistic theorems and the term "law" has been carried over to these theorems. There are other statistical and probabilistic theorems that also have "law" as a part of their names that have not obviously derived from empirical observations. However, both types of "law" may be considered instances of a scientific law in the field of statistics. What distinguishes an empirical statistical law from a formal statistical theorem is the way these patterns simply appear in natural distributions, without a prior theoretical reasoning about the data.

Contents

Examples

There are several such popular "laws of statistics".

The Pareto principle is a popular example of such a "law". It states that roughly 80% of the effects come from 20% of the causes, and is thus also known as the 80/20 rule. [2] In business, the 80/20 rule says that 80% of your business comes from just 20% of your customers. [3] In software engineering, it is often said that 80% of the errors are caused by just 20% of the bugs. [4] 20% of the world creates roughly 80% of worldwide GDP. [5] 80% of healthcare expenses in the US are caused by 20% of the population. [6]

Zipf's law, described as an "empirical statistical law" of linguistics, [7] is another example. According to the "law", given some dataset of text, the frequency of a word is inversely proportional to its frequency rank. In other words, the second most common word should appear about half as often as the most common word, and the fifth most common world would appear about once every five times the most common word appears. However, what sets Zipf's law as an "empirical statistical law" rather than just a theorem of linguistics is that it applies to phenomena outside of its field, too. For example, a ranked list of US metropolitan populations also follow Zipf's law, [8] and even forgetting follows Zipf's law. [9] This act of summarizing several natural data patterns with simple rules is a defining characteristic of these "empirical statistical laws".

Examples of empirically inspired statistical laws that have a firm theoretical basis include:

Examples of "laws" with a weaker foundation include:

Examples of "laws" which are more general observations than having a theoretical background:

Examples of supposed "laws" which are incorrect include:

See also

Notes

  1. ↑ Kitcher & Salmon (2009) p.51
  2. ↑ Bunkley, Nick (2008-03-03). "Joseph Juran, 103, Pioneer in Quality Control, Dies". The New York Times. ISSN   0362-4331 . Retrieved 2017-05-05.
  3. ↑ Staff, Investopedia (2010-11-04). "80-20 Rule". Investopedia. Retrieved 2017-05-05.
  4. ↑ Rooney, Paula (2002-10-03). "Microsoft's CEO: 80-20 Rule Applies To Bugs, Not Just Features". CRN. Retrieved 2017-05-05.
  5. ↑ 1992 Human Development Report. United Nations Development Program. New York: Oxford University Press. 1992.{{cite book}}: CS1 maint: others (link)
  6. ↑ "Percent of Total Health Care Expenses Incurred by Different Percentiles of U.S. Population: 2002". Research in Action. Issue 19: Figure 1. June 2006.
  7. ↑ Gelbukh & Sidorov (2008)
  8. ↑ Gabaix, Xavier (2011). "The Area and Population of Cities: New Insights from a Different Perspective on Cities" (PDF). American Economic Review. 101 (5): 2205–2225. arXiv: 1001.5289 . doi:10.1257/aer.101.5.2205. S2CID   4998367.
  9. ↑ Anderson, John R.; Schooler, Lael J. (November 1991). "Reflections of the Environment in Memory" (PDF). Psychological Science. 2 (6): 396–408. doi:10.1111/j.1467-9280.1991.tb00174.x. S2CID   8511110.

Related Research Articles

<span class="mw-page-title-main">Natural language processing</span> Field of linguistics and computer science

Natural language processing (NLP) is an interdisciplinary subfield of computer science and linguistics. It is primarily concerned with giving computers the ability to support and manipulate human language. It involves processing natural language datasets, such as text corpora or speech corpora, using either rule-based or probabilistic machine learning approaches. The goal is a computer capable of "understanding" the contents of documents, including the contextual nuances of the language within them. The technology can then accurately extract information and insights contained in the documents as well as categorize and organize the documents themselves.

<span class="mw-page-title-main">Probability theory</span> Branch of mathematics concerning probability

Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event.

<span class="mw-page-title-main">Pareto principle</span> Statistical principle about ratio of effects to causes

The Pareto principle states that for many outcomes, roughly 80% of consequences come from 20% of causes. Other names for this principle are the 80/20 rule, the law of the vital few or the principle of factor sparsity.

A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking. The process of contemplative and rational thinking is often associated with such processes as observational study or research. Theories may be scientific, belong to a non-scientific discipline, or no discipline at all. Depending on the context, a theory's assertions might, for example, include generalized explanations of how nature works. The word has its roots in ancient Greek, but in modern use it has taken on several related meanings.

<span class="mw-page-title-main">Benford's law</span> Observation that in many real-life datasets, the leading digit is likely to be small

Benford's law, also known as the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation that in many real-life sets of numerical data, the leading digit is likely to be small. In sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. If the digits were distributed uniformly, they would each occur about 11.1% of the time. Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.

<span class="mw-page-title-main">Infinite monkey theorem</span> Counterintuitive result in probability

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type any given text, including the complete works of William Shakespeare. In fact, the monkey would almost surely type every possible finite text an infinite number of times. The theorem can be generalized to state that any sequence of events which has a non-zero probability of happening will almost certainly eventually occur, given unlimited time.

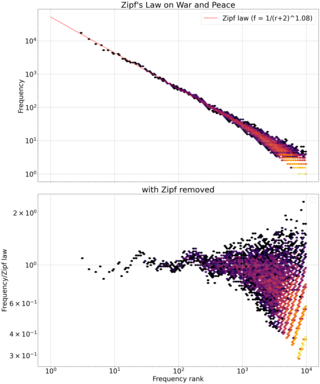
<span class="mw-page-title-main">Zipf's law</span> Probability distribution

Zipf's law is an empirical law that often holds, approximately, when a list of measured values is sorted in decreasing order. It states that the value of the nth entry is inversely proportional to n.

A law is a universal principle that describes the fundamental nature of something, the universal properties and the relationships between things, or a description that purports to explain these principles and relationships.

<span class="mw-page-title-main">Mathematical proof</span> Reasoning for mathematical statements

A mathematical proof is a deductive argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work.

<span class="mw-page-title-main">Heaps' law</span> Heuristic for distinct words in a document

In linguistics, Heaps' law is an empirical law which describes the number of distinct words in a document as a function of the document length. It can be formulated as

Empirical risk minimization is a principle in statistical learning theory which defines a family of learning algorithms based on evaluating performance over a known and fixed dataset. The core idea is based on an application of the law of large numbers; more specifically, we cannot know exactly how well a predictive algorithm will work in practice because we don't know the true distribution of the data, but we can instead estimate and optimize the performance of the algorithm on a known set of training data. The performance over the known set of training data is referred to as the empirical risk.

In statistics, classification is the problem of identifying which of a set of categories (sub-populations) an observation belongs to. Examples are assigning a given email to the "spam" or "non-spam" class, and assigning a diagnosis to a given patient based on observed characteristics of the patient.

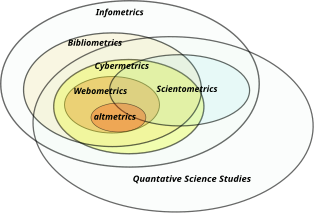
<span class="mw-page-title-main">Informetrics</span> Study of the quantitative aspects of information

Informetrics is the study of quantitative aspects of information, it is an extension and evolution of traditional bibliometrics and scientometrics. Informetrics uses bibliometrics and scientometrics methods to study mainly the problems of literature information management and evaluation of science and technology. Informetrics is an independent discipline that uses quantitative methods from mathematics and statistics to study the process, phenomena, and law of informetrics. Informetrics has gained more attention as it is a common scientific method for academic evaluation, research hotspots in discipline, and trend analysis.

<span class="mw-page-title-main">Rank–size distribution</span>

Rank–size distribution is the distribution of size by rank, in decreasing order of size. For example, if a data set consists of items of sizes 5, 100, 5, and 8, the rank-size distribution is 100, 8, 5, 5. This is also known as the rank–frequency distribution, when the source data are from a frequency distribution. These are particularly of interest when the data vary significantly in scales, such as city size or word frequency. These distributions frequently follow a power law distribution, or less well-known ones such as a stretched exponential function or parabolic fractal distribution, at least approximately for certain ranges of ranks; see below.

Quantitative linguistics (QL) is a sub-discipline of general linguistics and, more specifically, of mathematical linguistics. Quantitative linguistics deals with language learning, language change, and application as well as structure of natural languages. QL investigates languages using statistical methods; its most demanding objective is the formulation of language laws and, ultimately, of a general theory of language in the sense of a set of interrelated languages laws. Synergetic linguistics was from its very beginning specifically designed for this purpose. QL is empirically based on the results of language statistics, a field which can be interpreted as statistics of languages or as statistics of any linguistic object. This field is not necessarily connected to substantial theoretical ambitions. Corpus linguistics and computational linguistics are other fields which contribute important empirical evidence.

In natural language processing, textual entailment (TE), also known as natural language inference (NLI), is a directional relation between text fragments. The relation holds whenever the truth of one text fragment follows from another text.

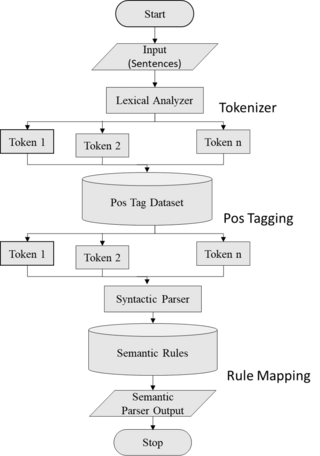
<span class="mw-page-title-main">Semantic parsing</span>

Semantic parsing is the task of converting a natural language utterance to a logical form: a machine-understandable representation of its meaning. Semantic parsing can thus be understood as extracting the precise meaning of an utterance. Applications of semantic parsing include machine translation, question answering, ontology induction, automated reasoning, and code generation. The phrase was first used in the 1970s by Yorick Wilks as the basis for machine translation programs working with only semantic representations. Semantic parsing is one of the important tasks in computational linguistics and natural language processing.

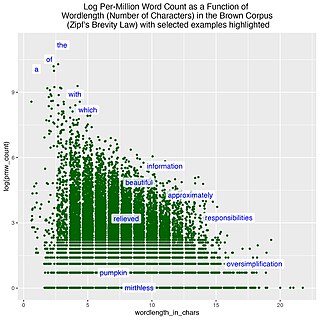
<span class="mw-page-title-main">Brevity law</span> Linguistics law

In linguistics, the brevity law is a linguistic law that qualitatively states that the more frequently a word is used, the shorter that word tends to be, and vice versa; the less frequently a word is used, the longer it tends to be. This is a statistical regularity that can be found in natural languages and other natural systems and that claims to be a general rule.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.