In the physical chemistry study of polymers, the end-to-end vector is the vector that points from one end of a polymer to the other end.
If each monomer unit in a polymer is represented by a point in space, the translation vectors connect between these points. The end-to-end vector is the sum of these translation vectors:
The norm of the end-to-end vector is called the end-to-end distance.
The quadratic mean of the end-to-end distance can be related to the quadratic mean of the radius of gyration of a polymer by the relation: [1]
In quantum mechanics, bra–ket notation, or Dirac notation, is used ubiquitously to denote quantum states. The notation uses angle brackets, and , and a vertical bar , to construct "bras" and "kets".
The Riesz representation theorem, sometimes called the Riesz–Fréchet representation theorem after Frigyes Riesz and Maurice René Fréchet, establishes an important connection between a Hilbert space and its continuous dual space. If the underlying field is the real numbers, the two are isometrically isomorphic; if the underlying field is the complex numbers, the two are isometrically anti-isomorphic. The (anti-) isomorphism is a particular natural one as will be described next; a natural isomorphism.
The Cauchy–Schwarz inequality is considered one of the most important and widely used inequalities in mathematics.
Radius of gyration or gyradius of a body about the axis of rotation is defined as the radial distance to a point which would have a moment of inertia the same as the body's actual distribution of mass, if the total mass of the body were concentrated there.
In mathematics, a quadric or quadric surface, is a generalization of conic sections. It is a hypersurface in a (D + 1)-dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in D + 1 variables. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a degenerate quadric or a reducible quadric.
Polymer physics is the field of physics that studies polymers, their fluctuations, mechanical properties, as well as the kinetics of reactions involving degradation and polymerisation of polymers and monomers respectively.
In physics, an operator is a function over a space of physical states onto another space of physical states. The simplest example of the utility of operators is the study of symmetry. Because of this, they are very useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory.
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential take the form of a plane wave modulated by a periodic function. Mathematically, they are written:
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component and the intrinsic covariant derivative component.
In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.
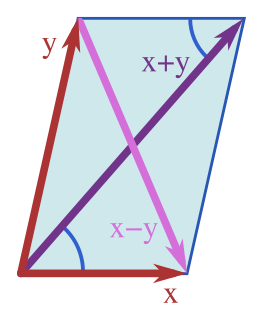
In linear algebra, a branch of mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. If a norm arises from an inner product then the polarization identity can be used to express this inner product entirely in terms of the norm. The polarization identity shows that a norm can arise from at most one inner product; however, there exist norms that do not arise from any inner product.
An ideal chain is the simplest model to describe polymers, such as nucleic acids and proteins. It only assumes a polymer as a random walk and neglects any kind of interactions among monomers. Although it is simple, its generality gives insight about the physics of polymers.
The worm-like chain (WLC) model in polymer physics is used to describe the behavior of polymers that are semi-flexible: fairly stiff with successive segments pointing in roughly the same direction, and with persistence length within a few orders of magnitude of the polymer length. The WLC model is the continuous version of the Kratky–Porod model.
The Debye–Waller factor (DWF), named after Peter Debye and Ivar Waller, is used in condensed matter physics to describe the attenuation of x-ray scattering or coherent neutron scattering caused by thermal motion. It has also been called the B factor or the temperature factor. Often, "Debye–Waller factor" is used as a generic term that comprises the Lamb–Mössbauer factor of incoherent neutron scattering and Mössbauer spectroscopy.
Rubber elasticity refers to a property of crosslinked rubber: it can be stretched by up to a factor of 10 from its original length and, when released, returns very nearly to its original length. This can be repeated many times with no apparent degradation to the rubber. Rubber is a member of a larger class of materials called elastomers and it is difficult to overestimate their economic and technological importance. Elastomers have played a key role in the development of new technologies in the 20th century and make a substantial contribution to the global economy. Rubber elasticity is produced by several complex molecular processes and its explanation requires a knowledge of advanced mathematics, chemistry and statistical physics, particularly the concept of entropy. Entropy may be thought of as a measure of the thermal energy that is stored in a molecule. Common rubbers, such as polybutadiene and polyisoprene, are produced by a process called polymerization. Very long molecules (polymers) are built up sequentially by adding short molecular backbone units through chemical reactions. A rubber polymer follows a random, zigzag path in three dimensions, intermingling with many other rubber molecules. An elastomer is created by the addition of a few percent of a cross linking molecule such as sulfur. When heated, the crosslinking molecule causes a reaction that chemically joins (bonds) two of the rubber molecules together at some point. Because the rubber molecules are so long, each one participates in many crosslinks with many other rubber molecules forming a continuous molecular network. As a rubber band is stretched, some of the network chains are forced to become straight and this causes a decrease in their entropy. It is this decrease in entropy that gives rise to the elastic force in the network chains.
Monte Carlo in statistical physics refers to the application of the Monte Carlo method to problems in statistical physics, or statistical mechanics.
In physics, a quantum amplifier is an amplifier that uses quantum mechanical methods to amplify a signal; examples include the active elements of lasers and optical amplifiers.
A polymer is a macromolecule, composed of many similar or identical repeated subunits. Polymers are common in, but not limited to, organic media. They range from familiar synthetic plastics to natural biopolymers such as DNA and proteins. Their unique elongated molecular structure produces unique physical properties, including toughness, viscoelasticity, and a tendency to form glasses and semicrystalline structures. The modern concept of polymers as covalently bonded macromolecular structures was proposed in 1920 by Hermann Staudinger. One sub-field in the study of polymers is polymer physics. As a part of soft matter studies, Polymer physics concerns itself with the study of mechanical properties and focuses on the perspective of condensed matter physics.
Polymerscattering experiments are one of the main scientific methods used in chemistry, physics and other sciences to study the characteristics of polymeric systems: solutions, gels, compounds and more. As in most scattering experiments, it involves subjecting a polymeric sample to incident particles, and studying the characteristics of the scattered particles: angular distribution, intensity polarization and so on. This method is quite simple and straightforward, and does not require special manipulations of the samples which may alter their properties, and hence compromise exact results.
In mathematics, the Frobenius inner product is a binary operation that takes two matrices and returns a number. It is often denoted . The operation is a component-wise inner product of two matrices as though they are vectors. The two matrices must have the same dimension - same number of rows and columns, but are not restricted to be square matrices.
