
Supervised learning (SL) is a paradigm in machine learning where input objects and a desired output value train a model. The training data is processed, building a function that maps new data to expected output values. An optimal scenario will allow for the algorithm to correctly determine output values for unseen instances. This requires the learning algorithm to generalize from the training data to unseen situations in a "reasonable" way. This statistical quality of an algorithm is measured through the so-called generalization error.

Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing.
In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector.
Hebbian theory is a neuropsychological theory claiming that an increase in synaptic efficacy arises from a presynaptic cell's repeated and persistent stimulation of a postsynaptic cell. It is an attempt to explain synaptic plasticity, the adaptation of brain neurons during the learning process. It was introduced by Donald Hebb in his 1949 book The Organization of Behavior. The theory is also called Hebb's rule, Hebb's postulate, and cell assembly theory. Hebb states it as follows:
Let us assume that the persistence or repetition of a reverberatory activity tends to induce lasting cellular changes that add to its stability. ... When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.
In signal processing, independent component analysis (ICA) is a computational method for separating a multivariate signal into additive subcomponents. This is done by assuming that at most one subcomponent is Gaussian and that the subcomponents are statistically independent from each other. ICA was invented by Jeanny Hérault and Christian Jutten in 1985. ICA is a special case of blind source separation. A common example application of ICA is the "cocktail party problem" of listening in on one person's speech in a noisy room.
Ridge regression is a method of estimating the coefficients of multiple-regression models in scenarios where the independent variables are highly correlated. It has been used in many fields including econometrics, chemistry, and engineering. Also known as Tikhonov regularization, named for Andrey Tikhonov, it is a method of regularization of ill-posed problems. It is particularly useful to mitigate the problem of multicollinearity in linear regression, which commonly occurs in models with large numbers of parameters. In general, the method provides improved efficiency in parameter estimation problems in exchange for a tolerable amount of bias.
The forward algorithm, in the context of a hidden Markov model (HMM), is used to calculate a 'belief state': the probability of a state at a certain time, given the history of evidence. The process is also known as filtering. The forward algorithm is closely related to, but distinct from, the Viterbi algorithm.
Random forests or random decision forests is an ensemble learning method for classification, regression and other tasks that works by creating a multitude of decision trees during training. For classification tasks, the output of the random forest is the class selected by most trees. For regression tasks, the output is the average of the predictions of the trees. Random forests correct for decision trees' habit of overfitting to their training set.

In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable in the input dataset and the output of the (linear) function of the independent variable. Some sources consider OLS to be linear regression.
In mathematics, a Relevance Vector Machine (RVM) is a machine learning technique that uses Bayesian inference to obtain parsimonious solutions for regression and probabilistic classification. The RVM has an identical functional form to the support vector machine, but provides probabilistic classification.
Oja's learning rule, or simply Oja's rule, named after Finnish computer scientist Erkki Oja, is a model of how neurons in the brain or in artificial neural networks change connection strength, or learn, over time. It is a modification of the standard Hebb's Rule that, through multiplicative normalization, solves all stability problems and generates an algorithm for principal components analysis. This is a computational form of an effect which is believed to happen in biological neurons.
The generalized Hebbian algorithm (GHA), also known in the literature as Sanger's rule, is a linear feedforward neural network for unsupervised learning with applications primarily in principal components analysis. First defined in 1989, it is similar to Oja's rule in its formulation and stability, except it can be applied to networks with multiple outputs. The name originates because of the similarity between the algorithm and a hypothesis made by Donald Hebb about the way in which synaptic strengths in the brain are modified in response to experience, i.e., that changes are proportional to the correlation between the firing of pre- and post-synaptic neurons.
In statistics and machine learning, ensemble methods use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone. Unlike a statistical ensemble in statistical mechanics, which is usually infinite, a machine learning ensemble consists of only a concrete finite set of alternative models, but typically allows for much more flexible structure to exist among those alternatives.
In machine learning, the kernel perceptron is a variant of the popular perceptron learning algorithm that can learn kernel machines, i.e. non-linear classifiers that employ a kernel function to compute the similarity of unseen samples to training samples. The algorithm was invented in 1964, making it the first kernel classification learner.
Multiple kernel learning refers to a set of machine learning methods that use a predefined set of kernels and learn an optimal linear or non-linear combination of kernels as part of the algorithm. Reasons to use multiple kernel learning include a) the ability to select for an optimal kernel and parameters from a larger set of kernels, reducing bias due to kernel selection while allowing for more automated machine learning methods, and b) combining data from different sources that have different notions of similarity and thus require different kernels. Instead of creating a new kernel, multiple kernel algorithms can be used to combine kernels already established for each individual data source.
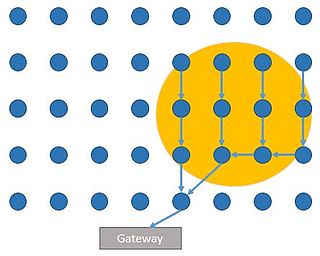
Wireless sensor networks (WSN) are a spatially distributed network of autonomous sensors used for monitoring an environment. Energy cost is a major limitation for WSN requiring the need for energy efficient networks and processing. One of major energy costs in WSN is the energy spent on communication between nodes and it is sometimes desirable to only send data to a gateway node when an event of interest is triggered at a sensor. Sensors will then only open communication during a probable event, saving on communication costs. Fields interested in this type of network include surveillance, home automation, disaster relief, traffic control, health care and more.
Mixture of experts (MoE) is a machine learning technique where multiple expert networks (learners) are used to divide a problem space into homogeneous regions. MoE represents a form of ensemble learning.
In machine learning, knowledge distillation or model distillation is the process of transferring knowledge from a large model to a smaller one. While large models have more knowledge capacity than small models, this capacity might not be fully utilized. It can be just as computationally expensive to evaluate a model even if it utilizes little of its knowledge capacity. Knowledge distillation transfers knowledge from a large model to a smaller one without loss of validity. As smaller models are less expensive to evaluate, they can be deployed on less powerful hardware.
A graph neural network (GNN) belongs to a class of artificial neural networks for processing data that can be represented as graphs.
In deep learning, weight initialization describes the initial step in creating a neural network. A neural network contains trainable parameters that are modified during training: weight initalization is the pre-training step of assigning initial values to these parameters.










